射频技术简介
射频(RF)技术简介
RF(Radio Frequency)技术被广泛应用于多种领域,如:电视、广播、移动电话、雷达、自动识别系统等。专用词RFID(射频识别)即指应用射频识别信号对目标物进行识别。RFID的应用包括:
● ETC(电子收费)
● 铁路机车车辆识别与跟踪
● 集装箱识别
● 贵重物品的识别、认证及跟踪
● 商业零售、医疗保健、后勤服务等的目标物管理
● 出入门禁管理
● 动物识别、跟踪
● 车辆自动锁死(防盗)
RF(射频)专指具有一定波长可用于无线电通信的电磁波。电磁波可由其频率表述为:KHz(千赫),MHz(兆赫)及GHz(千兆赫)。其频率范围为VLF(极低频)也即10-30KHz至EHF(极高频)也即30-300GHz。
RFID是一项易于操控,简单实用且特别适合用于自动化控制的灵活性应用技术,其所具备的独特优越性是其它识别技术无法企及的。它既可支持只读工作模式也可支持读写工作模式,且无需接触或瞄准;可自由工作在各种恶劣环境下;可进行高度的数据集成。另外,由于该技术很难被仿冒、侵入,使RFID具备了极高的安全防护能力。
从概念上来讲,RFID 类似于条码扫描,对于条码技术而言,它是将已编码的条形码附着于目标物并使用专用的扫描读写器利用光信号将信息由条形磁传送到扫描读写器;而RFID则使用专用的RFID读写器及专门的可附着于目标物的RFID单元,利用RF信号将信息由RFID单元传送至RFID读写器。
RFID单元中载有关于目标物的各类相关信息,如:该目标物的名称,目标物运输起始终止地点、中转地点及目标物经过某一地的具体时间等,还可以载入诸如温度等指标。RFID单元,如标签、卡等可灵活附着于从车辆到载货底盘的各类物品。
RFID技术所使用的电波频率为50KHz-5.8GHz,如图一所示,一个最基本的RFID系统一般包括以下几个部份:
● 一个载有目标物相关信息的RFID单元(应答机或卡、标签等)
● 在读写器及RFID单元间传输RF信号的天线
● 一个产生RF信号的RF收发器(RF transceiver)
● 一个接收从RFID单元上返回的RF信号并将解码的数据传输到主机系统以供处理的读写器。
● 天线、读写器、收发器及主机可局部或全部集成为一个整体,或集成为少数的部件。不同制造商有各自不同的集成方法。
(在以上基本配置之外,还应包括相应的应用软件)
典型的射频电路
射频电路最主要的应用领域就是无线通信,图1为一个典型的无线通信系统的框图,下面以这个系统为例分析射频电路在整个无线通信系统中的作用。
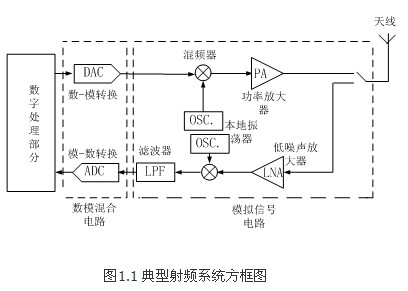
这是一个无线通信收发机(<span>tranceiver)的系统模型,它包含了发射机电路、接收机电路以及通信天线。这个收发机可以应用于个人通信和无线局域网络中。在这个系统中,数字处理部分主要是对数字信号进行处理,包括采样、压缩、编码等;然后通过A/D转换器转换器变成模拟形式进入模拟信号电路单元。
射频电路的组成和特点
下面,将针对图方框图中的低噪声放大器(LNA)讨论一般射频电路的组成和特点。


上图给出了这个放大器的电路板图, 注意到输入信号是通过一个经过匹配滤波网络输入放大模块。放大模块一般采用晶体管的共射极结构,其输入阻抗必须与位于低噪声放大器前面的滤波器的输出阻抗 相匹配,从而保证最佳传输功率和最小反射系数,对于射频电路设计来说,这种匹配是必须的。此外,低噪声放大器的输出阻抗必须与其后端的混频器输入阻抗相匹 配,同样能保证放大器输出的信号能完全、无反射的输入到混频器中去。这些匹配网络是由微带线组成,在有些时候也可能由独立的无源器件组成,但是它们在高频 情况下的电特性与在低频的情况下完全不同。图上还可以看出微带线实际上是一定长度和宽度的敷铜带,与微带线连接的是片状电阻、电容和电感。
射频电路的功率和增益
增益、噪声和非线性是描述射频电路最常用的指标。在射频和微波系统中,由于反射的普遍存在和理想的短路、开路难以获得,低频电路中常用的电压和电流参数的测量变得十分困难,因此,功率的测量得到了广泛的应用。并且,传统的射频和微波电路使用分立元件和传输线构成,电路的输入、输出通常需要匹配到一个系统阻抗(50?或75?)。由于上面两个原因,电路的性能指标,如增益、噪声、非线性等,都可以通过功率表示出来
为了计算方便,在射频和微波工程中常用功率强度对数的形式来表示功率,dBm是信号功率相对于1mW的对数值。
有了功率的定义,现在开始讨论射频系统中的一个重要指标:增益。在射频系统中考虑的功率指的是功率增益,这与电压增益很容易产生混淆。此外,在射频系统中,同样存在多种功率的定义,当匹配电路存在时,可以定义以下功率:
PL:负载获得的功率
Pin:电路的输入功率
Pavs:信号源能提供的最大功率
Pavn:电路能提供的最大功率
相应的,可以定义三种功率:一般功率增益Gp、转化功率增益GT和资用增益GA,它们由下列公式给出。



