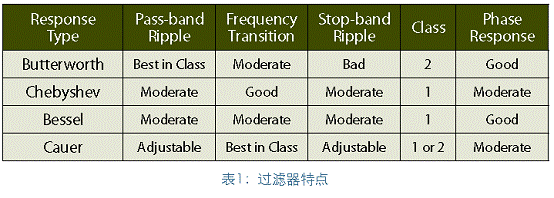
Butterworth是最常见的滤波器类型，因为其具有相比其他任何滤波器来说，最精密的平顶通带。Butterworth属于二类滤波器，意味着波纹被限制在阻带内。
Chebshev是一类滤波器，响应曲线比Butterworth更为陡峭，但是它在通带内会受到波纹的影响。
Cauer频率响应可以是一类，也可以是二类，因为在通带和阻带中的波纹都可以独立调整。对于给定的波纹值，它在阻带和通带之间具有最快的增益跃迁。
Bessel频率响应适合于需要线性相位响应的系统，并且在通带中具有最大的平坦群延时。因此，在波形保持非常重要的音频电路中很受欢迎。
频率的斜率
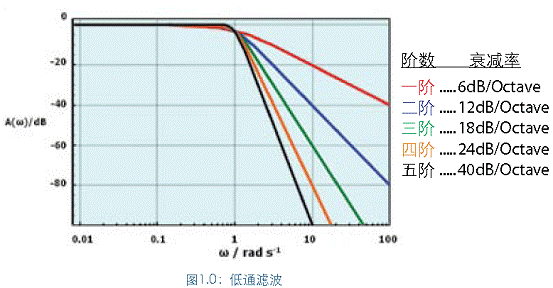
电路中电抗性元件的个数，不论是电感性还是电容性元件，决定了电路中的“阶”数。一个电阻加上一个电容就是第一阶，并且加入到电路中的每个电抗性组件都会相应增加一阶。当频率相同时，每一阶会让斜率变得更大，每八度增加6dB。
滤波器的阶数越高，响应曲线越接近垂直，如图1.0所示。
模拟或数字
采用数字方案要取决于许多因素；数字方案通常会花费较长的开发时间，需要更多的资源，并且可能无法达到与模拟滤波器相同的性价比。使用数字滤波器的器件，比如FPGA或CPU，需要将模拟信号转换成数字信号以进行滤波，然后再重新转换成模拟信号。DSP解决方案能提供复杂处理的能力，但是这种额外的灵活性需要更多的开发工作和更高的花费。
在做出决定以前，主要应该考虑的是设计中其他必要功能模块的复杂性。
滤波器设计的传统方式
拉普拉斯变换可以通过计算或从标准响应曲线公式中进行更为普遍的查找来实现。
公式1.0是针对三阶Butterworth滤波器进行的变换，其中：s=o+i。w，（实数+复数部分）变换分子和分母可以进行分解因子计算，以找到公式的极点与零点。 使用极点和零点的滤波稳定性 极点是能够使分母为0（或H（s）=无穷大）的“s”的数值，“零点”是能够让分子为0的 “s” 的数值。为了使滤波器稳定，极点的数值必须大于零点的数值。由于公式1.0只有极点存在，表明该三阶Butterworth稳定，并且没有摆动。 如果滤波器的时间相对振幅响应需要进行检验，则对公式可以进行反拉普拉斯变换，以使其回到时间域。没有必要在模拟 “s”平面和“z”平面之间进行转换，因为已经可以使用数字方案了。 Sallen-Key有源滤波器 尽管许多不同的配置可以在数学关系的基础上用于设计最终的电路，但由于本文章的目的，我们选择了Sllen-Key二极滤波器，因为它在所有针对低通和高通过滤的二阶滤波器配置中是最受欢迎的。它们构造简单，并且对于组件容差有相对弹性。图2.0和2.1分别展示了低通和高通配置。
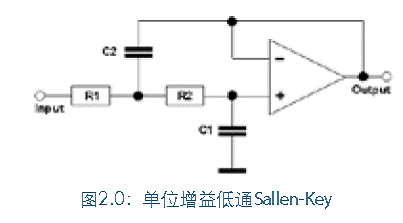
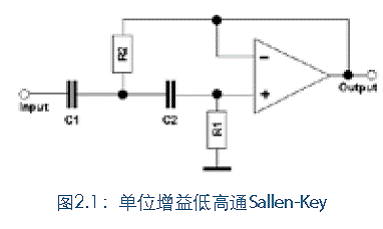通过调整组件的值，任何二阶低通响应都可以产生。
针对模拟滤波的单芯片解决方案
如果需要高阶滤波器，基于Sallen-Key的滤波器可能不是最好的方案。达到8阶的滤波器就有可能使用专用的开关电容型滤波器，比如美信（Maxim）的MAX293。将输入时钟频率转换为所需要的滚升/滚降频率使得这些都变得非常灵活，但是它们受到的干扰确实要高于连续时间滤波器。
TI的UAF42和美信的MAX274滤波器的优势是将低通，高通和带通合并在一个单独的元件中。通过使用高度准确的内部微调电容，它们就不容易受频率变化的影响，而频率变化会导致各级间的不一致。
希望能实时改变滤波器规格的工程师可能会考虑现场可编程模拟阵列（FGAA），例如来自于Anadigm的产品。这些产品采用小型QFN封装，具有可完全配置的模拟更能模块。例如，AN121E04具有4个可配置I/O单元和两个专用的输出单元，因此可以并行处理多个模拟信号。
 |
 |
