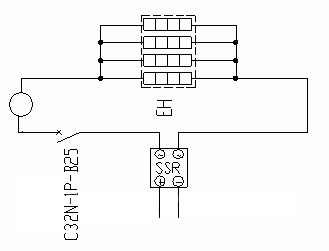
基本微分电路,仅是一原理性的微分电路,是不能付诸实用的。其原因为,微分电路本质上是一种高通滤波器,对于高出工作频率以上的噪声,有更大的增益,将无用的噪声放大,故高频噪声干扰很严重。运算放大器本身在高频时有滞后的附加相移,R2、和C1组成的反馈系统,在高频时会进一步产生滞后的相移,就会使整个系统不稳定和产生自激振荡。
解决这个问题的最简单办法是在微分电容上串一个电阻R1,如图5.4-13A所示。

在图5.4-13A所示的电路中加入了电阻R1,就能消除自激振荡和抑制高频噪声的干扰,但是它会影响微分电路的运算精度。R1的值越大,引进运算误差越大。由于图5.4-13A电路进一步加接了电容C2,这能使R1选取更小些,从而提高运算精度,并且它有相位超前特性,在R1较小的情况下仍能消除自激振荡。
由图5.4-13B所示的实际微分电路的幅频波特图中看出,当仅是加入R1时,在WH以上高频范围内增益将保持在A1=R2/R1,加上C1后,R1C1,R2C2,就会使WH以上高频范围内的增益特性以DB/10倍频速率下降,这时有
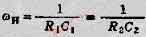
只要W《WH,电路就相当于理想微分器。这时输出电压

所以作为微分,理所当然的用在W〈WH以下范围。