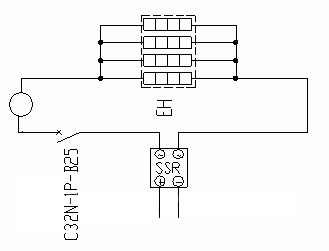
低通滤波器设计首先根据给定技术条件,选择某一形式的低通原则型滤波器,查出、计算归一化元件值,然后用所有要求的截止频率和负载电阻进行标定,便可得到所需要低通滤波网络。
1、滤波器特性的逼近 理想化的低通滤波器衰减特性是不可能实现的,实际上只能以尽可能小的误差去逼近它,当选用不同的逼近函数便可得到不同响应曲线,即不同的衰减特性的滤波器,经常采用的逼近函数特性有以下几种:
1)巴特沃兹滤波器 又称最平响应滤波器,通带内幅度最平埙,通带外上升缓慢。
2)切比霸夫滤波器 又称等波纹响应滤波器,通带内呈等波纹起伏,通带外衰减单调上升。
3)考尔滤波器 又称通阻带等波纺响应滤波器,通带、阻带内均呈等波起伏,其过渡带衰减上升最快,但设计计算很繁琐,网络结构复杂。
4)贝塞尔滤波器 双称最平时延滤波器,具有最大平坦群时延特性。
2、归一化低通原型滤波器频率和阻抗的结合标定通常,都将低通原型滤波器的阻抗和频率作归一化处理,使得滤波器设计通用化。工程设计中查表得到的是频率和阻抗都已归一化的元件值,根据设计要求还要标定成实际需要的截止频率O。和负载电阻RL(或电源内阻)时的元件值。实际值按下列公式计算;
式中R、L、C、O为实际值1 R1、L1、C1、O为归一化值。
3、综合网络的对称性 用网络综合法设计 巴特沃兹和切比霸夫低通原型滤波器,得到的网络结构形式为T型其对形式X型,如表5.1-2底部和顶部示出的两个对偶网络。这两个网络的响应曲线是一致的,在电气上是等效的,即满足同一要求的低通滤波器都有具有两种结构,设计者可根据要求选定其中一种。一般选电感小的电路,国为电感体积在频率低时较大,损耗较大,制造工艺比电容复杂,且歇易受外界电磁场干扰。
欲将已知T型网络变换为其对偶形式,网络结构和元件特性作如下变化;
(1)串联支路变为并联支路,反之亦然;
(2)并联元件变为串联元件,反之亦然;
(3)电感变为电容,电容变为电感,而元件值不变,即a(H)变a(F);电阻变为电导,而数值不变,即B(O)变为B(S),开路变为短路,电流源变为电压源,反之亦然。
图5.1-4示出由已知T型网络变换为其对偶形式的例子。
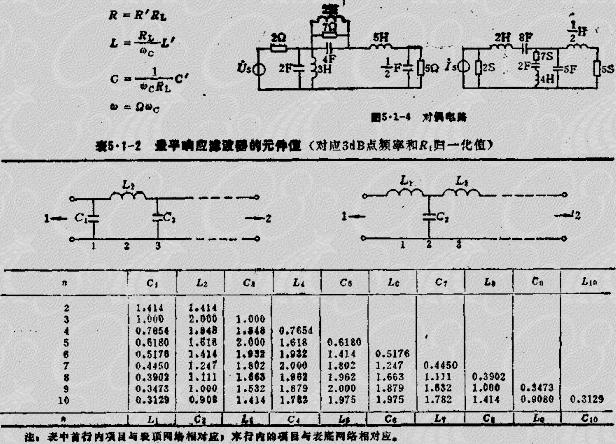
巴特沃兹低通滤波器在零频率上有最佳的衰减特性逼近。
当考虑截止频率为任意频率OP(即基准频率为任意频率OP)时的衰减特性如图5.1-5所示。




切比雪夫低通滤波器设计
切比雪夫低通滤波器,在通带内衰减呈现等起伏特性,起伏的大小标志着衰减对理想均匀特性的最大偏离,而阻带内以更大的增长速率衰减。
对于匹配型切比雪夫低通滤波器,传输函数的模平方和衰减分别为
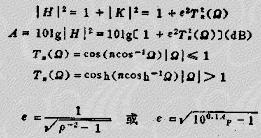
式中|K|2为特征函数的模平方;T。(R)为切比雪夫多项式;N为切比雪夫多项式的阶数,也就是滤波器的阶段;R为归一频率,R=W/WP;WP为截止频率;AP为截止频率R=1上的衰减;C为在截止频率R=1上反射系数或衰减;C为在截止频率R=1上反射系数或衰减的度量。
下面只给出奇阶切比雪夫滤波器设计计算的一般形式,因为滤波器两端电阻之比R1/R2完全取决于直流反射系数P(O)或直流衰减A(O),由于奇阶切比雪夫滤波器的A(O)=O或P(O)=O,所以R2=R1。表5.1-4示出这类滤波器的设计步骤和举例。
对于偶阶切比雪夫滤波器,相应的直流衰为A(O)=101G(1+C2)=AP
即A(O)等于在截止频率R=1上的衰减AP,从即|P(O)|等于在R=1上的反射系数P,所以A(O)或P(O)均不相等,必须通过适当的频率变换,得到这类滤波器的一种变换型,才可以应用R2=R1的情况进行分析和计算,请参考文献(1)
滤波器的频率变换与网络转换应用网络综合法设计滤波器时,一般只设计各种类型低通原型滤波器,而高通、带通和带阻滤波器则可以由低通原型滤波器,借助频率变换原理,通过网络转换而得到。从频率原理来看,选择一个适当的变换式,将低通响应曲线变换为高通、带通





及带阻响应曲线,经过网络转换实现变换后的各类滤波器,其元件参数由低通原型滤波器元件参数值来表示,参见表5.1-5、表5.1-6、表5.1-7。