模拟电路网络课件 第十四节:放大电路的频率响应
在实际应用中,电子电路所处理的信号,如语音信号、电视信号等都不是简单的单一频率信号,即是具有一定的频谱的复杂信号。这些复杂信号是由一些幅度及相位都有固定比例关系的多频率分量组合而成的。
由于放大电路中存在电抗元件(如管子的极间电容,电路的负载电容、分布电容、耦合电容、射极旁路电容等),当信号频率较高或较低时,不但放大倍数会变小,而且会产生超前或滞后的相移,使得放大电路对不同频率信号分量的放大倍数和相移都不同。
如果放大电路对不同频率信号的幅值放大不同,就会引起幅度失真;如果放大电路对不同频率信号产生的相移不同就会引起相位失真;幅度失真和相位失真总称为频率失真或线性失真。 ——电压放大倍数的幅值与频率 ![]() 的函数关系,称为幅频响应——放大倍数的相位
的函数关系,称为幅频响应——放大倍数的相位![]() 与频率的函数关系称为相频响应。
与频率的函数关系称为相频响应。
2、RC耦合放大器的幅频特性
RC耦合放大器的幅频特性曲线如图所示。我们将全频域分为三个频区:中频区、高频区、低频区。
中频区:在一个较宽的频率范围内,曲线是平坦的。即放大倍数不随信号频率而变。(在此频率范围内,耦合电容、射极旁路电容视为短路,极间电容视为开路)。中频区放大倍数用AVM表示。
高频区(f 高于fH的频率范围):当信号频率升高时,放大倍数随频率的升高而减小。(在此频率范围,幅频特性主要受BJT的极间电容的影响)。
低频区(f 低于fL的频率范围):当频率降低时,放大倍数随频率的降低而减小。(在此频率范围,幅频特性主要受耦合电容和旁路电容的影响)。
上限截止频率(fH):当AV下降为0.707AVM时所对应的高端信号频率;
下限截止频率(fL):当AV下降为0.707AVM时所对应的低端信号频率。
通频带(BW):fH和fL之间的频率范围称为放大电路的通频带或带宽。
BW=fH-fL
3、波特图
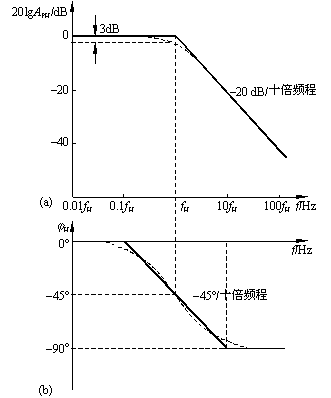
在研究放大电路的频率响应时,由于信号的频率范围很宽(从几赫到几百兆赫以上),放大电路的放大倍数也很大(可达百万倍),为压缩坐标,扩大视野,在画频率特性曲线时,频率坐标采用对数刻度,而幅值(以dB为单位)或相角采用线性刻度。在这种半对数坐标中画出的幅频特性和相频曲线称为对数频率特性或波特图。如低通电路的波特图如图所示。
3.7.1 单时间常数RC电路的频率响应
一、RC低通电路的频率响应
由于放大电路高频区的频率响应可用图1所示的RC低通电路来模拟。下面我们分析RC低通电路的频率响应。
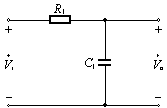 图1
图1
1、频率响应
![]() (1)
(1)
令![]() (2)
(2)
得 ![]() (3)
(3)
其中幅频响应为![]() (4)
(4)
相频响应为![]() (5)
(5)
2、幅频响应波特图
 图4
图4
根据式(4)幅频响应可在波特图中用两条直线来近似描述:
(1)当 ![]() 时
时
![]()
用分贝表示为: ![]()
(2)当![]() 时
时
![]()
用分贝表示为 ![]()
此直线的斜率为-20dB/十倍频程,它与零分贝线在![]() 处相交。近似的幅频响应如图2(a)所示。
处相交。近似的幅频响应如图2(a)所示。
3、相频响应
根据式(5)作出相频响应,它可用三条直线来近似描述:
(1)当![]() 时,
时, ![]() ,得一条
,得一条 ![]() 的直线。
的直线。
(2)当 ![]() 时 ,
时 , ![]() ,得一条
,得一条![]() 的直线。
的直线。
(3)当![]() 时,
时, ![]() 。
。
由于当 ![]() 或
或 ![]() 时,相应可近似得
时,相应可近似得 ![]() 和
和 ![]() ,故在
,故在 ![]() 和
和 ![]() 之间,可用一条斜率为
之间,可用一条斜率为 ![]() /十倍频程的直线来表示,于是可画得相频响应如图2(b)所示。
/十倍频程的直线来表示,于是可画得相频响应如图2(b)所示。
二、RC高通电路的频率响应
放大电路的低频响应,可用如图1所示的RC高通电路来模拟。下面我们分析RC高通电路的频率响应
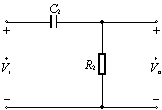 图1
图1
1、频率响应表达式
![]() (1)
(1)
令 ![]() (2)
(2)
![]() (3)
(3)
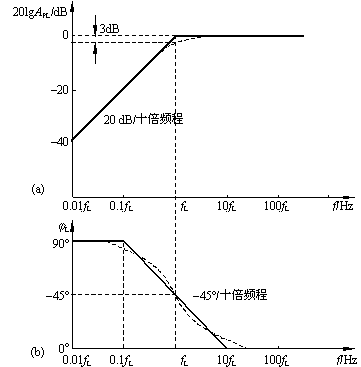 图2
图2
由式(3)可得
幅频响应为 ![]() (4)
(4)
相频响应为 ![]() (5)
(5)
2、波特图
采用与低通电路同样的折线似方法,可画出高通电路的幅频和相频响应波特图如图2所示
3.7.2 单级放大电路的高频响应
一、BJT高频小信号模型建模
1、BJT高频小信号模型的引出
根据BJT的特性方程,推导出的H参数低频小信号模型在高频运用的情况下,其物理过程有些差异,主要表现在BJT的极间电容不可忽略。为此,我们从BJT的物理机质出发加以分析,再用电阻、电容、电感等电路元件来模拟其物理过程,从而得出BJT的高频小信号模型,如图1所示。现就此模型中的各个元件参数作一简要的说明。
2、BJT的高频小信号模型:
在图示的BJT的高频小信号模型中
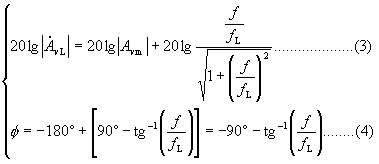
图1 BJT的高频小信号模型
——受控电流源 ,它受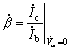 混合P型等效电路如图1所示。
混合P型等效电路如图1所示。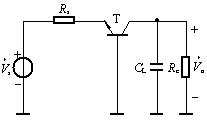
![]()
![]()
式中 ![]()
![]() 时
时![]()
 图2 所在回路的时间常数比
图2 所在回路的时间常数比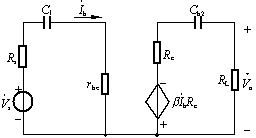 (
(  )的要小得 忽略。于是可得放大电路的高频小信号等效模型如图2所示。
)的要小得 忽略。于是可得放大电路的高频小信号等效模型如图2所示。
 关;
关; 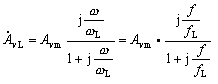 的影响不大。从
的影响不大。从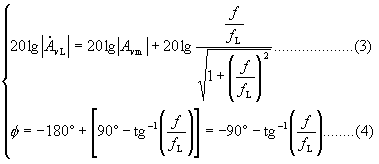 下降。而此时
下降。而此时  的容抗越大,则可视为开路,对
的容抗越大,则可视为开路,对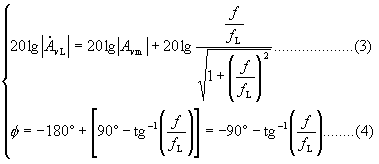 的影响不大。下降;而由于耦合电容C的存在,使低频时的
的影响不大。下降;而由于耦合电容C的存在,使低频时的 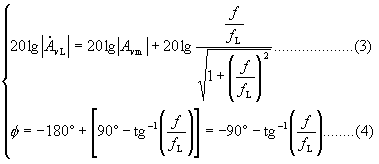 下降。
下降。 可视为开路;而
可视为开路;而  ,则
,则 ![]() 的作用,而耦合电容C 仍可视为短路,高频小信号等效电路如下图所示。
的作用,而耦合电容C 仍可视为短路,高频小信号等效电路如下图所示。 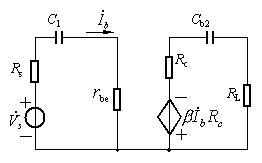

![]()

![]() 开路,而 考虑C的作用,可画出低频小信号等效电路如图所示。
开路,而 考虑C的作用,可画出低频小信号等效电路如图所示。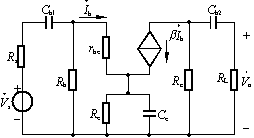

 (1) , (2)
(1) , (2)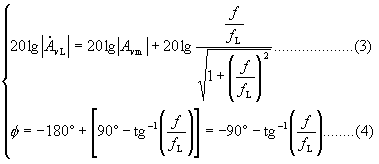 的近似式:
的近似式: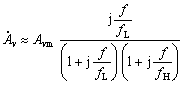 (1) 时,
(1) 时, ![]() ,
, ![]() ,则上式变为 就是中频放大倍数; ,上式变为为低频段的放大倍数; ),则
,则上式变为 就是中频放大倍数; ,上式变为为低频段的放大倍数; ),则 ![]() ,上式变为 为高频区的电压放大倍数。
,上式变为 为高频区的电压放大倍数。
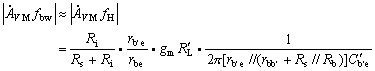 ,则
,则 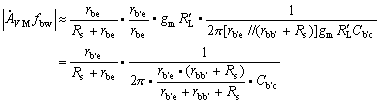
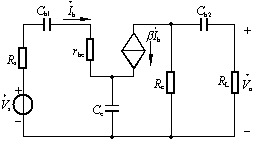
要分析电路的低频响应,首先画出它的低频小信号等效电路,如图1所示。

为便于分析对电路作以下作一些合理的近似,使其简化。
1、设 ![]() 远大于放大电路本身的输入阻抗,以致Rb的影响可以忽略;
远大于放大电路本身的输入阻抗,以致Rb的影响可以忽略;
2、Ce的值足够大 ![]()
于是可除去Re、Rb得简化电路如图2所示。
3、把Ce折算到基极电路,折算后的容抗为
![]()
即折算后的电容为
![]()
基极回路中的总电容C1
![]()
![]()
且一般 ,Ce的作用可忽略。这样可最后的简化电路图3。
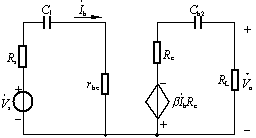
二、射极偏置电路下限频率
射极偏置电路简化后的低频等效电路如图所示,

由图可得
![]()
设中频区电压增益为
![]()
因此
![]()
式中
![]()
![]()
如果fL1和fL二者之间的比值在四倍以上,则可取较大的值作为放大电路的下限频率。
3.7.4 共基放大电路的高频响应
根据如图(a)所示的共基电路交流通路,可画出其高频小信号等效电路如图(b)所示。首先,我们来考察BJT电容Cb¢e和Cb¢c以及负载电容CL对高频响应的影响。


(a) 交流通路
(b) 高频小信号等效电路
一、Cb¢e的影响
由共基电路高频小信号等效电路可见,如果忽略rbb¢的影响,则Cb¢e直接接于输入端,输入电容Ci=Cb¢e,不存在密勒倍增效应,且与Cb¢c无关。所以,共基电路的输入电容比共射电路的小得多,fH1很高。理论分析的结果 ![]() 。
。
二、Cb¢c以及负载电容CL的影响
如果忽略rbb¢的影响,则Cb¢c直接接到输出端,也不存在密勒倍增效应。输出端总电容Cb¢c+ CL,输出回路时常数为 ![]() ,该输出回路决定的fH2为
,该输出回路决定的fH2为
![]()
如果![]() 和CL较大,则fH2较低。所以说,共基电路与共射电路一样,承受容性负载的能力较差,负载电容CL将成为制约共基电路高频响应的主要因素。而对于纯阻负载,共基电路的高频特性将非常好。
和CL较大,则fH2较低。所以说,共基电路与共射电路一样,承受容性负载的能力较差,负载电容CL将成为制约共基电路高频响应的主要因素。而对于纯阻负载,共基电路的高频特性将非常好。