引言
如果您已经阅读过博闻网中的路由器工作原理一文,您会了解到路由器的作用是管理网络流量和找到发送分组数据包的最佳路由。但是您是否想过路由器是怎么做到这一点的?路由器需要一些网络状态的信息来决定如何发送分组数据包以及发往哪里。但是它是怎样收集这些信息的?
在本篇博闻网文章中,我们将带您详细了解路由器需要哪些信息来决定往哪发送分组数据包。
路由器基础知识路由器使用路由算法来找到到达目的地的最佳路由。当我们说“最佳路由”时,我们考虑的参数包括诸如跳跃数(分组数据包在网络中从一个路由器或中间节点到另外的节点的行程)、延时以及分组数据包传输通信耗时。
关于路由器如何收集网络的结构信息以及对之进行分析来确定最佳路由,我们有两种主要的路由算法:总体式路由算法和分散式路由算法。采用分散式路由算法时,每个路由器只有与它直接相连的路由器的信息——而没有网络中的每个路由器的信息。这些算法也被称为DV(距离向量)算法。采用总体式路由算法时,每个路由器都拥有网络中所有其他路由器的全部信息以及网络的流量状态。这些算法也被称为LS(链路状态)算法。我们将在下一节讨论LS算法。
LS算法采用LS算法时,每个路由器必须遵循以下步骤:
- 确认在物理上与之相连的路由器并获得它们的IP地址。
当一个路由器开始工作后,它首先向整个网络发送一个“HELLO”分组数据包。每个接收到数据包的路由器都将返回一条消息,其中包含它自身的IP地址。
测量相邻路由器的延时(或者其他重要的网络参数,比如平均流量)。
为做到这一点,路由器向整个网络发送响应分组数据包。每个接收到数据包的路由器返回一个应答分组数据包。将路程往返时间除以2,路由器便可以计算出延时。(路程往返时间是网络当前延迟的量度,通过一个分组数据包从远程主机返回的时间来测量。)请注意,该时间包括了传输和处理两部分的时间——也就是将分组数据包发送到目的地的时间以及接收方处理分组数据包和应答的时间。
向网络中的其他路由器广播自己的信息,同时也接收其他路由器的信息。
在这一步中,所有的路由器共享它们的知识并且将自身的信息广播给其他每一个路由器。这样,每一个路由器都能够知道网络的结构以及状态。
使用一个合适的算法,确定网络中两个节点之间的最佳路由。
在这一步中,路由器选择通往每一个节点的最佳路由。它们使用一个算法来实现这一点,如Dijkstra最短路径算法。在这个算法中,一个路由器通过收集到的其他路由器的信息,建立一个网络图。这个图描述网络中的路由器的位置以及它们之间的链接关系。每个链接都有一个数字标注,称为权值或成本。这个数字是延时和平均流量的函数,有时它仅仅表示节点间的跃点数。例如,如果一个节点与目的地之间有两条链路,路由器将选择权值最低的链路。
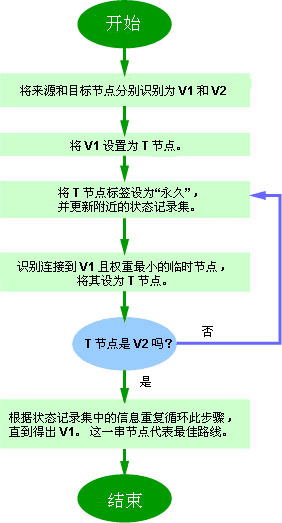
Dijkstra算法执行下列步骤:
- 路由器建立一张网络图,并且确定源节点和目的节点,在这个例子里我们设为V1和V2。然后路由器建立一个矩阵,称为“邻接矩阵”。在这个矩阵中,各矩阵元素表示权值。例如,[i, j]是节点Vi与Vj之间的链路权值。如果节点Vi与Vj之间没有链路直接相连,它们的权值设为“无穷大”。
路由器为网路中的每一个节点建立一组状态记录。此记录包括三个字段:
- 前序字段——表示当前节点之前的节点。 长度字段——表示从源节点到当前节点的权值之和。 标号字段——表示节点的状态。每个节点都处于一个状态模式:“永久”或“暂时”。
路由器初始化(所有节点的)状态记录集参数,将它们的长度设为“无穷大”,标号设为“暂时”。
路由器设置一个T节点。例如,如果设V1是源T节点,路由器将V1的标号更改为“永久”。当一个标号更改为“永久”后,它将不再改变。一个T节点仅仅是一个代理而已。
路由器更新与源T节点直接相连的所有暂时性节点的状态记录集。
路由器在所有的暂时性节点中选择距离V1的权值最低的节点。这个节点将是新的T节点。
如果这个节点不是V2(目的节点),路由器则返回到步骤5。
如果节点是V2,路由器则向前回溯,将它的前序节点从状态记录集中提取出来,如此循环,直到提取到V1为止。这个节点列表便是从V1到V2的最佳路由。
这些步骤的流程图如下:
在下一页中我们将使用这个算法具体分析一个示例。
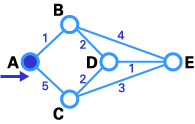
示例:Dijkstra算法我们想找到A与E(下图)之间的最佳路由。可以看到A与E之间有六条可能路径(ABE、ACE、ABDE、ACDE、ABDCE、ACDBE),很明显ABDE是最佳路由,因为它的权值最小。但是实际情况并非总是如此简单,有很多复杂的情形需要使用算法来找到最佳路由。
- 如下图所示,源节点(A)被选为T节点,所以它的标号是永久(我们将永久性节点以实圈标注,T节点以-->符号标注)。
在这一步中,直接链接到T节点的暂时性节点(B, C)的状态记录集已经被修改。同时,由于B有更小的权值,所以它被选作T节点,其标号被改为永久(如下图所示)。
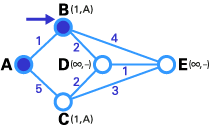
与步骤2类似,在这一步中,直接链接到T节点的暂时性节点(D, E)的状态记录集已经被修改。同时,由于D有更小的权值,所以它被选作T节点,其标号被改为永久(如下图所示)。
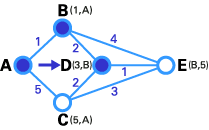
在这一步中,已经没有任何暂时性节点,所以我们仅仅需要确认下一个T节点。因为E有最小权值,所以它被选作T节点。
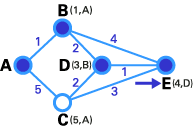
E是目的节点,所以我们在这里停止。
我们已经到达了终点!现在,我们需要确定路由。E的前序节点是D,D的前序节点是B,B的前序节点是A。所以最佳路由是ABDE。在这个案例中,权值和为4(1+2+1)。
虽然这个算法工作良好,但是它非常复杂,以致于路由器需要花费大量时间进行处理,网络的性能因此下降了。同样,如果一个路由器将错误的信息发送给其他路由器,那么所有的路由决定都将是无效的。为了更好的理解这个算法,下面给出由C语言编写的源代码:
#define MAX_NODES 1024 /*最大节点数 */#define INFINITY 1000000000 /*比所有最大路径都大的数 */int n,dist[MAX_NODES][MAX_NODES]; /*dist[I][j] 是从 i 到 j 的距离*/void shortest_path(int s,int t,int path[ ]){struct state { /*当前计算的路径 */int predecessor ; /*前序节点 */int length /*从源节点到当前节点的长度*/enum {permanent, tentative} label /*标号状态*/}state[MAX_NODES];int I, k, min;struct state * p;for (p=andstate[0];p < andstate[n];p++){ /*初始化状态*/p->predecessor=-1p->length=INFINITYp->label=tentative;}state[t].length=0; state[t].label=permanent ;k=t ; /* k 是初始工作节点 */do{ /*是从 k 开始的一条更好路径么?*/for I=0; I < n; I++) /*图有 n 个节点 */if (dist[k][I] !=0 andand state[I].label==tentative){ if (state[k].length+dist[k][I] < state[I].length){ state[I].predecessor=k; state[I].length=state[k].length + dist[k][I] }}/*找到具有最小权值的暂时性节点。*/k=0;min=INFINITY;for (I=0;I < n;I++) if(state[I].label==tentative andand state[I].length <min)=state[I].length; k=I; }state[k].label=permanent}while (k!=s);/*将路径复制到输出数组*/I=0;k=0Do{path[I++]=k;k=state[k].predecessor;} while (k > =0);}DV算法
DV算法也被称为Bellman-Ford路由算法和Ford-Fulkerson路由算法。在这些算法中,每个路由器都有一个路由表,用来表示到任何目的地的最佳路由。一个典型的路由器J的网络图以及路由表如下所示。
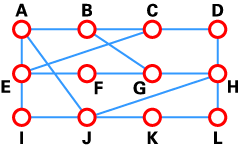
如表格所示,如果路由器J想发送分组数据包到路由器D,它应该将分组数据包先发送到路由器H。分组数据包到达路由器H后,它将检查自己的路由表来决定怎样将分组数据包发送到路由器D。
在DV算法中,每个路由器遵循以下步骤:
- 计算所有与本身直接相连的链接的权值并且将信息保存到路由器的路由表中。 一段时间后,路由器将其路由表发送给相邻路由器(不是所有的路由器),同时也收到每个相邻路由器的路由表。 根据其相邻路由器的路由表信息,路由器更新自己的路由表。
DV算法的一个最主要的问题是“无穷计数”。让我们通过一个例子来研究一下这个问题:
假设一个网络图如下所示。如图所示,A与网络的其他部分只有一条链路。所有节点的路由表以及网络图如下所示:
网络图和路由表
现在假设A 、 B之间的链路被剪断了。在这个时候,B修正了自己的路由表。经过一段时间后,路由器交换它们的路由表,因此B接收到了C的路由表。因为C不知道A 、B之间的链路上发生了什么事,所以它说它有一条权值为2的到A的链路(从C到B权值为1,从B到A权值为1——它不知道B已经没有到A的链路了)。B接收到路由表之后认为有另外一条链路从C到A,所以它修正了自己的路由表,即将无穷大更改为3(C认为,B到C权值为1,C到A权值为2)。路由器然后再一次交换它们的路由表。当C接收到B的路由表后,它发现B到A的链路权值从1更改为3,所以C更新了它的路由表,即将它到A的链路权值更改为4(根据B的描述,C到B权值为1,B到A权值为3)。
这个循环过程到最后,所有的节点发现到A的链路权值变成无穷大。这个情形如下表所示。因此,专家称DV算法具有低收敛率。
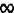 ,A
,A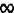
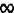
“无穷计数”问题
解决这个问题的一种方法是,路由器只发送信息给相邻路由器,且该相邻路由器不是通往目的地的唯一链接。比如在这个例子中,C就不应该发送任何关于A的信息给B,因为B是通往A的唯一路径。
分级路由可以看到,在LS和DV算法中,每个路由器都需要保存其他路由器的一些信息。随着网络规模的扩大,网络中的路由器也将增加。因此,路由表的规模也将增大,从而使路由器不能有效地处理网络流量。使用分级路由可以解决这个问题。让我们通过一个例子来说明一下。
我们使用DV算法来查找节点间的最佳路由。在下述情形中,网络中的每个节点保存了一个有17个记录的路由表。下面是A的一个典型网络图和路由表。
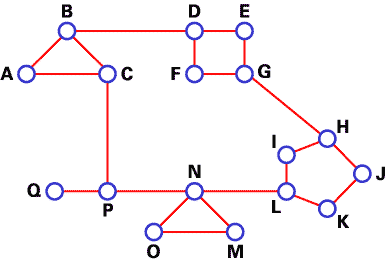
在分级路由中,路由器被分成很多组,称为区域。每个路由器都只有自己所在区域路由器的信息,而没有其他区域路由器的信息。所以在其路由表中,路由器只需要存储其他每个区域的一条记录。在这个例子中,我们将网络分为5个区域(如下图)。
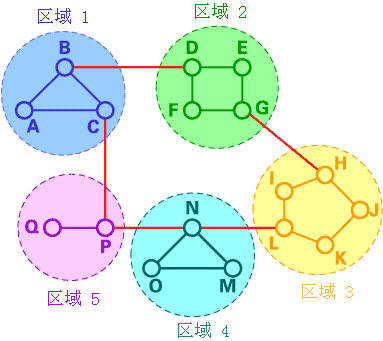
如果A想发送分组数据包到在区域2中的一个路由器(D、E、F或G),它就将分组数据包先发送到B,依此类推。可以看到,在这种类型的路由中,可以对路由表进行概括,因此网络效率提高了。上面的例子描述了一个两级的分级路由。同样我们也可以采用三级或者四级的分级路由。
在一个三级的分级路由中,网络被分为很多簇。每个簇由很多个区域组成,每个区域包含很多个路由器。分级路由广泛应用于互联网路由中,并且使用了多种路由协议。