摘要:基于蒙特卡罗实验原理,提出了一种针对适应型PID控制器的参数整定比较方法。对于若干典型热工对象,利用所提出的方法,研究了Xiegler-Nichols方法、Chien-Hrones-Reswick方法、Cohen-Coon方法、IMC方法、IST2E最优方法、极点配置方法、幅值相位裕量方法所设计的适应型PID控制系统的性能比较问题。
关键词:PID参数整定 自适应控制 蒙特卡罗方法
在控制理论和技术飞速发展的今天,PID控制由于其具有控制方法简单、稳定性好、可靠性高和易于现场调试等优点,被广泛应用于工业过程控制。在实际过程中,被控过程经常存在时变不确定性的特点,自适应PID控制是解决这一问题的有效途径。自适应PID控制的一种常用方案是通过在线辨识控制对象参数,根据一定的整定算法实时整定PID控制器参数。对于各种参数整定方法,核心问题是控制系统的稳定性、收敛性和鲁棒性。文献[1]、[2]基于一般对象,对几种典型的PID参数整定方法做过比较研究。对于热工对象,参数在有界的范围内变动,在设计自适应型PID控制器的时候,采用何种PID控制器数整定方法可得到较好的控制效果,还有待研究。本文针对经典Z-N法、Chien-Hrones-Reswick法、Cohen整定公式、极点配置法、内模法、IST2E最优整定算法和幅值相位裕量法(GPM)等PID参数整定算法、基于蒙特卡罗随机实验,定量分析了连续型适适应PID的性能鲁棒性,提出了适应型PID控制器参数整定的比较方法,并进行了实例研究。
1 PID控制器参数整定公式及比较方法
本文中涉及的PID整定方法的参数整定公式见表1,有关符号见文献[3]、[4]。
本文所研究对象为单变量系统,可用如下的传递函数表示:
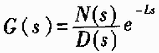
其中,N(s)与D(s)均为多项式,并且是互质的,N(s)阶数大于等于D(s),L为大于等于0的实数。所研究的被控制对象模型含有一定的不确定性,设其传递函数的参数在有界区域内变动,因此其模型是一个传递函数族,以{G(s)}表示。
所采用的PID型控制器的表达式如下:
u(s)=Kp(1+1/Tis+Tds)e(s)
其参数Kp、Ti、Td均为正实数,因此所有PID型控制器组成一个控制器集合,以{PID}表示。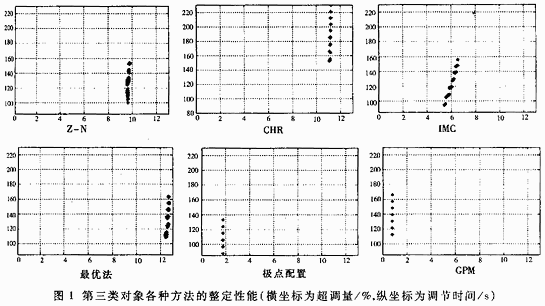
进行PID控制器设计时,通过某种PID整定方法可以获得控制器的三个参数,与被控制对象组成一个负反馈系统,其动态性能指标采用超调量σ%和调节时间Ts表示。当被控制对象的参数发生变化时,需要利用获得的新被对象参数,重新整定控制器参数。由于被控制对象是一个传递函数族,因此动态性能指标是一个集合,以下列符号表示:
{σ%,Ts}
可见这是一个二维向量的集合,是平面坐标图上的一个区域。该区域与原点的距离大小反馈所整定的控制系统性能指标的好坏。而该区域的大小,则反馈控制系统在对象参数变动下其性能指标的散布程度,反馈所整定的控制系统的性能鲁棒性。
PID参数整定的比较方法的具体步骤如下:
(1)确定所研究的被控制对象传递函数及其参数变化区间,构成一个传递函数族;
(2)确定要进行比较的PID整定方法,选取合适的试验次数N,保证当N取列大的值时,所得控制系统性能指标的散布程度不再有显著变化;
(3)选定一种PID整定方法;
(4)每次试验先根据随机抽取的原则在所建立的模型集合中得到一个具体的精确模型,根据模型的参数整定出PID控制器的参数,组成闭合回路,形成完整的PID控制系统进行试验,根据试验结果计算调节时间、超调量;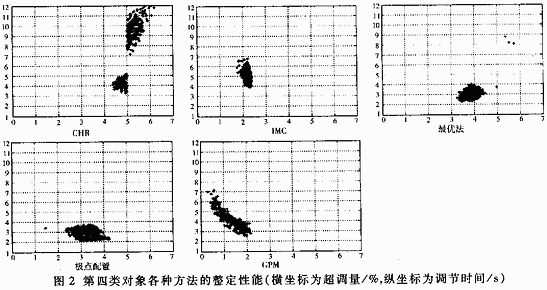
(5)重复步骤(4)N次,得到N组控制性能参数,根据这N组结果在坐标图上做出N个点的分布图;
(6)根据不同的整定方法重复步骤(3)~(5);
(7)根据所得到的结果比较各种整定方法的整定效果以及鲁棒性。
2 仿真研究及结果比较分析
热工模型一[5]:G(s)=k/(1+sT)n
取T:16~24s,k:0.8~1.2,n=3,仿真结果如图1所示,性能参数如表2所示。
表1 第三类对象各种整定方法性能参数表
| 经典Z-N法 | CHR法 | Cohen法 | |
| 超调量/% | 9.55~9.81(9.68) | 11.1~11.2(11.2) | 20.0~20.5(20.3) |
| 调节时间/s | 99.4~154(131) | 152~230(189) | 80.2~130(105) |
| IMC法 | 最优法(IST2E) | 极点配置法 | 幅值相位裕量法 |
| 5.40~6.56(6.08) | 12.4~12.7(12.6) | 1.76~1.79(1.79) | 0.786~0.795(0.792) |
| 93.4~156(126) | 108~162(135) | 87.3~134(113) | 112~166(141) |
平均值由所有实验结果的和除以实验次数得出,反映整定方法的平均整定效果。Cohen法的超调量较大,未在图1中列出。从上面的结果可以看出,几种方法中,GPM法和极点配置法整定效果较好。从超调量来看,整定效果依次为GPM法、极点配置法、IMC法和Z-N法、CHR法、IST2E最优法和Cohen法。从调节时间来看,整定效果依次为Cohen法、极点配置法、IMC法、Z-N法和IST2E最优法、GPM法和CHR法。Cohen法虽然调节时间比较短,但其超调量比较大。从点的散布程序来看,IMC法超调量跨度较大,CHR法调节时间跨度相对较大。
热工模型二[5]:G(s)=[k(-s+a)]/[(1+sT1)(1+sT2)]
取T1:4~6s,T2:0.32~0.48s,a:1~1.5,k:4.8~3.2,仿真结果如图2所示,性能参数如表3所示。
表2 第四类对象各种整定方法性能参数表
| 经典Z-N法 | CHR法 | Cohen法 | |
| 超调量/% | 不稳定 | 4.40~6.20(5.16) | 部分发散 |
| 调节时间/s | 不稳定 | 3.26~12.0(7.85) | 部分发散 |
| IMC法 | 最优法(IST2E) | 极点配置法 | 幅值相位裕量法 |
| 1.76~2.38(2.20) | 3.27~5.74(3.88) | 2.34~4.23(3.28) | 0.319~2.17(1.33) |
| 3.87~6.78(5.06) | 2.29~8.76(3.10) | 2.11~3.71(2.88) | 1.33~7.14(4.19) |
这里的GPM法取幅值裕量为5,相位裕量为60度。根据上述结果,从超调量来看,整定效果依次为GPM法、IMC法、极点配置法、IST2E最大法和CHR法。从调节时间来看,整定效果依次为极点配置法、IST2E最优法、GPM法、IMC法和CHR法。从整定性的散布情况来看,CHR法性能点比较分散,表明CHR法的整定性能随对象模型参数的变化较大,GPM法的调节时间跨度较大,而其它几种方法随对象参数的变化比较小。
3 再热器温度控制实例研究及分析
某电厂200M