三、牛顿流体及非牛顿流体
在节流装置的设计标准、规程以及一些流量测量方法的“适用范围”栏目中，常常提出所测流体仅限于“牛顿流体”。什么是牛顿流体和非牛顿流体呢? 在前述流体的粘度一节中，给出了流体动力粘度的定义式(1—3)，由该式可以导出在流体内部有速度梯度(剪切进度) 
时，作用在与该速度梯度方向垂直的单位面积上的内摩擦力(或称剪切应力、粘滞力) 
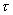与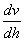 
之间的关系式是：
式(1—8)称牛顿粘性定律。当式中比例系数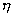 
(即动力粘度)为常数时，内摩擦力 
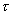与速度梯度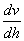 
间呈线性关系。这一规律的流体即称牛顿流体．不同种类的牛顿流体的比例常数 
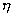值
各不相同。当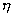 
值不是常数或 
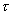与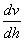 
间的关系不符式(1—8)所示规律，即不符牛顿粘性定律时，该流体即称非牛顿流体。一般高粘滞性流体和高分子溶液都呈现非牛顿流体的性质。典型的非牛顿流体以可塑性流体、膨胀性流体和宾厄姆(BINGham)流体为代表．其 
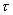与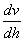 
的关系可用下列两个简单的典型式表示：
当式(1—9)中常数n＞I时，称可塑性流体；当n＜1时，称膨胀性流体．对宾厄姆流体，表达式为
式中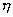 
B——常数，称塑性粘度；
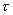h——流体开始流动时的内摩接力(剪切应力)，常称为屈服值。
为直观起见，常以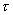 
作纵坐标，以 
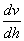为横坐标，绘出 
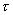与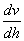 
的关系曲线，称流动曲线。对牛顿流体，流动曲线为通过原点的直线；对非牛顿流体，流动曲线有各种不同的形状。例如可塑性流体的流动曲线是下弯的曲线；膨胀性流体则是向上弯的曲线；宾厄姆流体为不通过原点的直线。
四、绝热指数及等熵指数
测量气(汽)体流量时，需要了解流体流经流量测量元件(例如节流元件)时的状态变化，为此需要知道被测气(汽)体的绝热指数和等熵指数。
流动工质在状态变化(由一种状态转变到另一种状态)过程中若不与外界发生热交换，则该过程称为绝热过程。若绝热过程没有(或不考虑)摩擦生热，即为可逆绝热过程．根据熵的定义，在可逆绝热过程中熵(S)值不变(S＝常数)，故可逆的绝热过程又称为等熵过程。例如，流体流经节流元件时，因为节流元件很短，其与外界的热交换及摩擦生热均可忽略，所以该过程可近似认为是等熵的．在此过程中，流体的压力P与比容V的X次方的乘积为常数，即PVX＝常数，X称为等熵指数。当被测气(汽)体服从理想气体定律时，等熵指数等于比热比，即定压比热Cp与定容比热Cv之比值Cp／Cv。在绝热过程中，比热比又叫绝热指数。
实际气(汽)体的等熵指数与介质的种类以及所处的压力、温度有关，可从有关手册的图表上查取．几种常用气体在常温常压下的X值见表l—8。至今还有许多气体或蒸汽的等熵指数尚没有数据发表，在此情况下可暂时用比热比代替。混合气体的等熵指数不服从叠加规律，但其定压比热和定容比热服从叠加规律，可按叠加法则求得，然后再求出混合气体的比热比．
五、可压缩流体的压缩系数
任何流体都可压缩，这是流体的基本属性。但在工程上液体一般可忽略其体积的微小变化，视为不可压缩①。对于气体，通常作为可压缩流体来处理。在流量测量中，气体流经测量元件的时间很短，来不及与外界进行热交换，且可不考虑摩擦生热，所以这时发生的气体状态变化过程可近似地视为可逆绝热过程或等熵过程。因此，可用绝热过程状态方程来计算不同状态下的比容(V)或密度(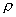 
)．但由于PVX＝常数这一绝热方程的形式用来换算不同状态下的比容或密度很不方便，在工程上仍用 
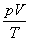＝mR(常数)这个理想气体状态方程式，只是再加一个实际气体偏离理
想气体的校正系数，这称为压缩系数(K0)．此时，气体状态变化的基本关系式为
因为V＝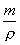 
（m――气体的质量； 
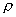――气体的密度），所以
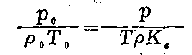
或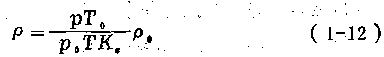 
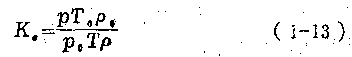
式中 P、T、V、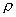 
——分别表示被测气体的绝对压力(Pa)，绝对温度(K)，在P、T状态下的容积(m3)和密度(kg／m3)；
P0、T0、V0、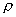 
0——分别表示被测气体在已知状态时的参数，一般情况下取P0＝1．0×l. 0 325×l05 Pa，T0＝273．15K。
由式(1—13)，压缩系数K0的物理意义就很明确，即根据理想气体状态方程求得的气体容积和实际气体间在各种压力、温度下有不同程度的偏离。压缩系数就是衡量这种偏差程度的尺度。不同的气体，压缩系数也不同。各种气体的压缩系数可由有关工程手册所载曲线查取，至于混合气体的压缩系数，可按下式确定：
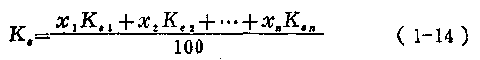
式中 X1，X2，…Xn——混合气体各组成部分所占容积的百分比；
K01，K02，…，K0n——混合气体各组成部分的压缩系数。
K0值确定后，即可代入式(1—12)，根据某一已知状态下的密度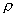 
。值求出任一状态下的密度 
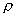．只有求出实际工作状态下的密度 
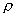，才能正确地求得该流体的流量．
—————————————————————
①压力较高及测量准确度要求较高时，需考虑液体的可压缩性。
