0 引言
温度控制是自动控制领域中最常见的问题之一，它涉及采暖、日常生活热水、化工生产、炼钢炼铁、造纸、矿山冶炼等各行业。加热源有煤、油、天然气、感应加热及电热管加热等，由于电加热方式所需设备简单、无污染及无噪音等优点而倍受人们青睐。近年来随着单片机、计算机及自动控制技术的发展和应用，一改有触点的传统控制方式，应用单片机组成高精度智能化温控仪已成为电加热温度控制的趋势和潮流。基于此，本文应用自动控制、智能控制和PWM技术，提出了一种构成高精度智能温度控制仪的控制算法。
1 控制对象数学模型的建立
1.1 对象特性
以生活热水加热系统为例，设被控对象温度为T，环境温度为 
，供热量为 
，散热量为 
为散热系数，A为散热面积，则能量平衡式
（1）
式中：M为水的质量； 
为水的比热。
将 
代入（1）式，整理得
(2)
设 
为对象的供热时间常数， 
为对象的供热比例系数，则得对象特性的微分方程为
(3)
式（3）表明了对象温度与供热能量及环境温度之间的关系，式中 
为变量。
1.2 对象传递函数分析
一般情况下，在不太长的一段时间内 
为不变量，则（3）式变为
（4）
对式（4）作拉氏变换，推出被测温度与供热(超调量)之间的传递函数为
（5）
1.3 对象的飞升曲线
对于上述电加热系统（不加控制器、开环），当给定值处于平衡后，加一阶跃电压（220V），其飞升曲线如图1所示。
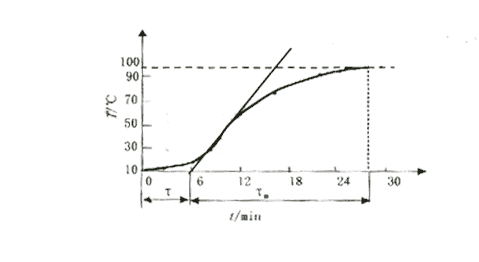
图1 温控对象的飞升曲线
由图1可求得对象的滞后时间为 
，对象的时间常数 
。故对象的传递函数可表示为一阶惯性环节加纯滞后环节[2]
2 控制算法的确定
2.1 史密斯纯滞后补偿原理
由以上分析过程看出，生活热水电加热系统由一典型的一阶惯性环节加纯滞后环节构成。一阶惯性环节采用典型的带积分分离的PID数字控制器即可满足要求，但控制对象的纯滞后性质常引起系统产生超调或振荡，从而使系统的稳定性降低。因此，可考虑应用史密斯预估器加以解决。上述单回路控制系统如图2所示，其中D(s)为调节器的传递函数， 
为被控对象的传递函数， 
为被控对象中不包含纯滞后环节部分的传递函数， 
为被控对象纯滞后部分的传递函数。
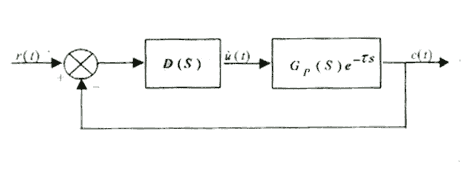
图2 带纯滞环节的控制系统
史密斯纯滞后补偿原理是：与D(s)并接一补偿环节 
，用来补偿被控对象中的纯滞后部分，这个环节称为预估器，如图3所示。
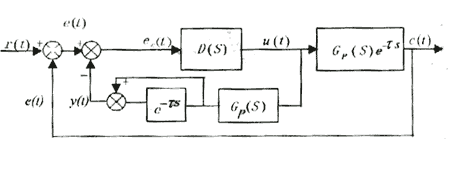
图3 带史密斯预估器的控制系统
整个纯滞后补偿器的传递函数为
经补偿后，系统的传递函数为
