1．卡门涡街的产生与现象
为说明卡门涡街的产生，我们来考虑粘性流体绕流圆柱体的流动．当流体速度很低时，流体在前驻点速度为零，来流沿圆柱左右两侧流动，在圆柱体前半部分速度逐渐增大，压力下降，后半部分速度下降，压力升高，在后驻点速度又为零．这时的流动与理想流体统流圆柱体相同，无旋涡产生，如图3—7a所示．
随着来流速度增加，圆柱体后半部分的压力梯度增大，引起流体附面层的分离，如图3—7b所示．当来流的雷诺数Re再增大，达到40左右时，由于圆柱体后半部附面层中的流体微团受到更大的阻滞，就在附面层的分离点S处产生一对旋转方面相反的对称旋涡．如图3－7c所示．
在一定的留诺数Re范围内，稳定的卡门涡街的及旋涡脱落频率与流体流速成正比．
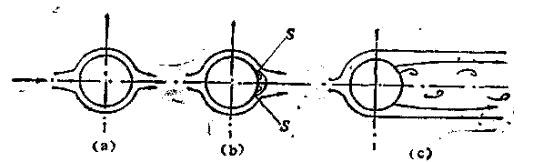
图3－7 圆柱绕涡街产生示意图
2．卡门涡街的稳定条件
并非在任何条件下产生的涡街都是稳定的．冯·卡门在理论上已证明稳定的涡街条件是：涡街两列旋涡之间的距离为h，单列两涡之间距离为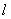 
，若两者之间关系满足
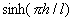＝1
或 h /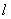 
＝0. 281 （3－24）
时所产生的涡街是稳定的。
3．涡街运动速度
为了导出旋涡脱落频率与流速之间的关系，首先要得到涡街本身的运动速度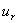 
．为便于讨论，我们假定在旋涡发生体上游的来源是无旋、稳定的流动，即其速度环量为零．从汤姆生定理可知，在旋涡发生体下游所产生的两列对应旋涡的速度环量 
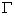，必然大小相等，方向相反，其合环量为零，由于对应两涡的旋向相反，速度环量大小相等，所以在整个涡群的相互作用下，涡街将以一个稳定的速度 
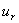向上游运动．从理论计算可得． 
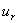的表示式为
＝ 
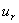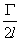tan h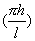 
(3-25)
对于稳定的涡街，将式（3－25）代入，有：
= 
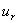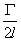tan h(0. 281 
)= 
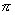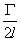
(3-26)
4．流体流速与旋涡脱落频率的关系
从前面讨论可知，当流体以流速u流动时，相对于旋涡发生体，涡街的实际向下游运动速度为u－ur．如果单列旋涡的产生频率为每秒f个旋涡，那么，流速与频率的关系为
u－ur = fl (3－27)
将式(3－26)代入，可得到流速u与旋涡脱落频率f之间的关系．但是，在实际上不可能测得速度环量 
的数值，所以只能通过实验来确定来流速度u与涡街上行速度ur之间的关系，确定因注形旋涡发生体直径d与涡街宽度h之间的关系，有：
h＝1. 3d （3－28）
ur＝0. 14u （3－29）
将式（3－24），（3－27），（3－28），（3－29）联立，可得：
f＝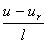 
＝ 
＝ 
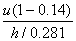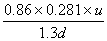（3－29’）
0. 2u / d
也可将上式写成：
St＝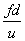 
0. 2 (3－30)
St称为斯特罗哈数．从实验可知，在雷诺数Re为3×l02－3×l05范围内，流体速度u与旋涡脱落频率的关系是确定的．也就是说，对于圆柱形旋涡发生体，在这个范围内它的斯特罗哈数St是常数，并约等于0．2，与理论计算值吻合的很好．对于圆柱型式的旋涡发生体，其斯特罗哈数St也是常数，但有它自己的数值．图3－8为圆往型旋涡发生体产生的涡街结构．
