模型与仿真基础

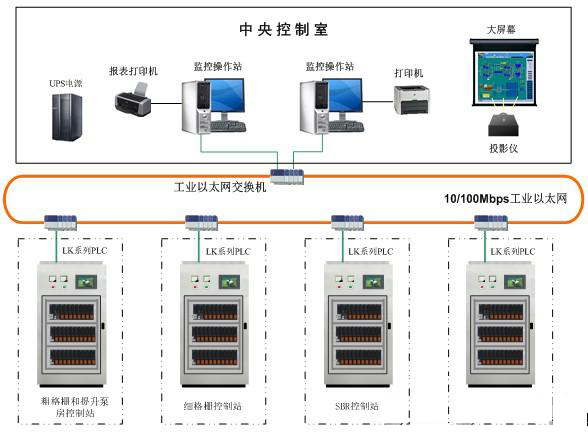
　　依靠数学模型和仿真，工程师可以对连续性的过程控制系统进行模拟测试，并根据测试推算系统以后的运行情况。
　　可塑模型和陶土模型展现的是对象的外形特征，和这种模型不同，过程模型则反映受控系统的操作过程以及对外界干扰的响应情况。通常，过程模型都可以用数学方程来确定系统输入量和输出量之间的关系。

图1：通过这个简单的模型，可以推算出，当水以每分钟F立方米
的速率填充一个底半径为R米的圆柱体水箱，t 分钟后水面高度L
（单位：米） 是多少。

　　模型可以有效地帮助我们分析PID回路，也可以为过程控制系统的设计提供参照。举个例子来说，如图1所示，是给一个圆柱形水箱充水的过程。假设水流入的速率是F，在t分钟后，水箱里的水面高度为：
　　[1] 
　　其中，R是水箱底部圆的半径。这样一个模型可以用来推算，若要装满整个水箱，控制器需要运行多长时间。
　　模型的要素
　　过程模型越复杂，包括的变量就越多，他们之间的数学关系也更加复杂，但不管系统多复杂，凡是连续过程的模型都包括以下四个基本要素：
　　■输入变量;
　　■输出变量;
　　■常数项
　　■算法
　　输出是在开发模型时，通过输入量的值分析得出的

预期值。在填充水箱的例子中，输出量L就可以由输入量t和F的值推算出来。
　　常数R的值取决于水箱的大小。一般情况下，常数是反映各基础科学的基本原理的常量，如物理学、化学、经济学、几何学等，它决定着过程的基本性能，而且这些常数是恒定不变的，不会因输入输出值随时间的变化而变化。
　　算法包括多种数学运算方法，主要是用来根据输入和常量值推算输出值。简单的像乘法和乘方，如方程[1]所示；复杂的如拉普拉斯变换和统计分配定律。
　　控制模型
　　过程模型可以为设计、执行、反馈控制测试提供有效的帮助。大多数解析法需要一个含增益和时间常数在内的模型，通过监测系统的反馈和响应速度，来判断该控制系统的控制性能。当对模型参数有一定了解后，工程师可以给过慢的进程增加一个响应较快的控制器，或是给过快的进程增加一个较慢的控制器，以达到预期的效果。
　　同样，模拟预测控制器可以用数学模型来测定控制系统的性能，以判断受控变量是否精确的达到了控制要求。在运行过程中通过比较得出的反馈，可以进行自我调整。
　　即使某控制方案是基于某特殊应用而开发的，在进行实际应用之前，也可以利用过程模型在虚拟环境下对该控制方案进行测试。模型的控制方程可以直接编程写入，也可以几种常用仿真语言中的任意一种或者自定义码写入专用的调试机中。在计算机上进行仿真，可以更快的发现该控制方案中的不足，也不用担心会对真实的工程造成任何损失。
　　模型开发实例
　　不管用途是什么，建立模型的诀窍就是把系统的运行状态用一系列的控制方程表示出来，如方程[1]所示。以"倒置的单摆模型"为例，如图所示，在地面上固定一个弹簧，弹簧顶端固定安放一个重物。水平方向的力使该物体在一个弧形范围内来回摆动。
　　这个模型的运行状态经过变形可以被应用于多个仿真研究。可以把它看成一个儿童玩具，也可以把它看成某高层建筑物在风中摇晃的缩影。加上一个接头，也可以近似看成是人在迈腿大步行走时腿部的动作。
　　无论是哪种情况，基本原理都是相同的。弹簧对物体的弹力和物体自身的重力是相对的。如果将物体和弹簧合起来，看成是一个质心离地面H米，质量为m千克的联合装置，整个装置的运动状态就可以用含有弧度q的方程式表示，如图所示。
　　实际应用检测
　　正如这个装置的简化过程一样，这个模型是逼近现实的模拟。假定不存在任何外力影响物体的运动，如摩擦力等，而弹簧对物体的弹力也与角坐标θ完全成比例。另外还要假定，该运动过程是从一个绝对垂直位置开始的（即θ的初始值为零）。
　　由于当θ无穷小时，q和sin(θ)的值近似相等。用q替换sin(θ)方程式[2]可以简化成方程式[3]，根据式[3]画出关于θ的趋势图，得到一条斜率为-（k- mg）/mh的直线，因此式[3]为关于θ的线性方程。
　　倒置单摆模型
　　[2]
　　简化后的倒置单摆模型
　　[3]
　　对简化模型方程求解
　　[4]
　　由上式解得
　　[5]
　　[6]
　　角速度变量的θ”是角速度θ的二次导数，t为该物体从初始位置到现在的运动时间，θ'0是物体在外力作用下的初始角速度，A是物体摆动的振幅，ω为振动的频率。A和ω是两个值取决于k，m，g，h和θ'的常量，如等式[5]和等式[6]所示。

　　方程式[3]真正的价值在于，通过它可以得到一个θ关于时间的趋势图，根据趋势图，我们可以预测该过程以后的运行状态。这个碰巧是一个只用方程式[3]这种线性方程就可以解决的问题。实际上，对方程式[3]进行求解，我们也可以得到关于θ（t）的表达式，如方程式[4]所显示。

图2：该弹簧装置的总质量为m千克，质心离地高度为h 米，且正好在弹簧支

点位置。弹簧装置在水平外力的作用下，从一个绝对垂直位置开始做弧形运动。该装置的重力mg.sin(θ)
和弹簧产生的弹力K下相对且互相平衡。其中常数g和k分别代表重力加速度和弹簧弹力系数。

　　相比之下，含有正弦函数的非线性方程，像方程[2]，对这种类似闭环系统的方程求解就相对复杂一些。很多时候，为了简化数学运算，工程师往往花更多的时间和精力去建立一个线性模型而不是非线性的。
　　局限性
　　不过，简化后的方程式[3]在精确的控制输出变量θ(t)上，并不是特别的有效。因为和实际操作过程不同，它所包含的输入变量不是一个可改变的量，而实际过程中，操作人员可能会赋予物体新的位移或新的速度。
　　即使对这个过程以及模型加以修一定的局限性。因为，只有在产生的摆动幅度小到足以使θ近似地和sin(θ)相等时，简化得出的方程式[3]才有效。否则，系统的的真实运行状态应该按照方程式[2]进行计算。
　　实际运行中，运行状态通常会因输入和输出的改变而变化，例如，当变量从极低值升高到极高值，再从极高值慢慢回落的过程中，大多数运行状态会因此而改变。在水箱填充这个实验中，当液位填充到箱体凸出不平的位置，这个模型也将失效。所以，过程模型中必须考虑到这些可能出现的变动，否则，依靠这些未经改善的模型进行操作，不可能达到预期的控制效果。
　　另外，在倒置单摆模型中，如果初始条件没有被准确的记录下来，方程[3]也不可能准确描述该装置的实际运动状态。在这个模型里，唯一的初始条件就是θ'0，它反映了物体在在初始时间t=0时，受到外力作用产生的初始角速度。式[6]可以看出θ'的值对物体摆动的振幅的影响。受到外力所产生的初始角速度θ'0越大，则物体每一次摆动的振幅A就会越大。
　　尽管如此，如果θ'的测量值有误差，那么根据该模型所计算出的振幅也将和物体的实际状况出现偏差。同样，如果物体不是严格的从绝对垂直位置（即θ(0)=0的位置）出发，对模型的行为预测也将出现偏差。在应用过程中，为了让实际运行状态和通过模型测试推算出的状态完全符合，控制工程师通常将系统的所有初始条件设置为零，以避免因初始条件的偏差而造成结论推算的误差。
　　仿真结果
　　不过，当这些限制条件可以被确认并被削弱到极小的时候，就可以离用过程模型对实际状况进行相当准确的仿真。在已知过程的运行状况的前提下，工程师会将模型放入到各种可能出现的环境中，进行有代表性的一系列测试，以保证系统精度。
　　例如，当风突然变大，大厦将会摇晃的更加厉害。对倒置的单摆模型加以修改，增加初始扰动（θ’0），即增加初始的角速度，也可以模拟出一个类似的测试环境。式[6]可以看出，振幅A和初始速度θ’0成正比，当初始速度增加，振幅也将相应的增加，正如实际情况中大厦的情况一样。
　　仿真最大的优点在于，可以在实际操作从没尝试过的环境中进行测试。特别是，在仿真过程中，可能发现一些没考虑到意外状况，可能是在实际应用中必须避免的危险情况；也可能是当前系统还需要改进的漏洞。当基于一个有效的模型进行仿真时，工程师就可以从反复的试验和误差调试中，完善并整合系统运行必须的各种条件（如温度、压力、流速等），大大的降低生产成本。
　　翻译：常嘉

文章编号：070301
　　发送短信“文章编号+评语代码”至13816124995，告诉我们您对此文的意见。
　　1- 很好，有很高的参考价值
　　2- 一般，有一定的参考价值
　　3- 不好，没有参考价值