摘 要: 本文介绍了虚拟仪器技术及其开发语言LabWindows/CVI, 并结合自己开发的异步电机空载试验采集处理系统讨论了虚拟仪器在电机试验领域的应用。
关键词: 虚拟仪器 LabWindows/CVI 空载试验 数据采集与处理
前 言
虚拟仪器是全新概念的最新一代测量仪器,它将传统仪器由硬件电路实现的数据分析与显示功能改由功能强大的计算机及其显示器来执行,它是按照测量原理采用适当的信号分析技术和处理技术编制某种测量功能的软件就构成了该种功能的测试仪器。因此,如果我们在电机型式试验中引入虚拟仪器,利用计算机强大的处理功能,开发出完全替代真实测量工具的虚拟仪器对试验进行自动采集并实现试验的自动处理和生成报告。可以看出，虚拟仪器这一全新测量仪器在传统的电机试验应用上将带来重大影响。
虚拟仪器VI及其编程语言LabWindows/CVI
虚拟仪器(Virtual Instrument,简称VI)是现代计算机技术和仪器技术深层次的结合。随着计算机技术和仪器技术的发展，由硬件电路实现的信号处理功能正逐步由软件替代。虚拟仪器是以软件为核心，由计算机及必要的硬件组建起来的测试系统或仪器系统，在计算机上对虚拟仪器面板的操作与现实中的仪器面板操作一样。在虚拟仪器中，用户可以自己设计或定义新的理论和新的算法来适应不同的测量需求，仪器的功能更加灵活、强大，所以有“软件就是仪器”的说法。因此,虚拟仪器是计算机硬件资源、仪器与测控系统硬件资源和虚拟仪器软件资源的有效结合。
虚拟仪器的实质是利用计算机显示器模拟传统仪器的控制面板,以多种形式输出检测结果,利用计算机软件实现信号数据的运算、分析和处理，利用I/O接口设备完成信号的采集、测量和调理,从而完成各种测试功能的一种计算机仪器系统。操作者使用鼠标或键盘操作虚拟面板就如同使用一台专用测量仪器。
虚拟仪器的硬件包括计算机和I/O接口设备。计算机可以是一台PC机或者工作站,它是硬件平台的核心。I/O接口设备主要完成被测输入信号的采集、放大、模/数转换。按照总线的不同可以分为PC总线的DAQ(数据采集卡/板) 、GPIB总线仪器和VXI总线仪器等等。
虚拟仪器的编程语言有多种。LabWindows/CVI是其中最优秀的语言之一，它是美国NI(National Instruments)公司开发的32位面向计算机测控领域的软件开发平台。它以ANSI为核心,将功能强大的、使用灵活的C语言平台与数据采集、分析和表达等测控专业工具有机结合,它支持事件驱动与回调函数编程技术,它的集成化开发平台、交互式编程方法、丰富的功能面板和库函数大大增强了C语言的功能,为熟悉C的开发人员开发检测、数据采集、过程监控等系统提供了一个理想的软件开发环境。
可以看出,虚拟仪器这一适合测控领域的开发平台完全适合于电机试验领域。引入虚拟仪器将改善电机试验测量的适时性要求,提高仪器仪表的精度并可以自己开发特殊要求的仪器,利用计算机的处理功能可以实现试验后数据的自动处理和报表,当然也可以实现试验数据的数据库管理。
虚拟仪器的异步机空载试验采集处理系统
虚拟仪器的电机试验应用程序结构
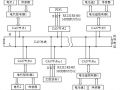
以LabWindows/CVI开发平台设计的基于PC-DAQ的虚拟仪器测试系统为例,其在电机试验领域应用的系统结果如图所示:
  |
|
数据采集卡 |
设备驱动 |
虚拟仪器面板 |
|
应用程序 | ||
|
LabWindows/CVI函数 | ||
|
LabWindows/CVI平台 | ||
|
计算机 | ||
由传感器接受被测信号转换为电量信号,送入信号处理电路进行整形、转换和滤波处理,变成标准信号,数据采集卡采集信号处理电路的电压信号,转换为计算机能处理的数字信号,经过设备驱动程序数字信号送入计算机在LabWindows/CVI平台下调用信号处理函数,编写程序和设计虚拟仪器面板,形成不同针对试验的测量处理系统。
异步机空载采集处理系统
异步电机空载试验计算机处理的数学模型
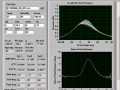
异步电机的空载试验是在被试电机空载运行时测量三相电压、三相电流、功率,作出电压-电流、电压平方-空载损耗、电压-功率的关系曲线, 在电压-电流曲线上我们查出额定电压的空载电流值，在电压-功率的曲线上我们查出额定电压的空载损耗值，结合电压平方-空载损耗曲线分离出铁耗和风摩耗值。
因此，曲线拟合的表达式是决定我们处理空载损耗的关键。参考电机学相关书籍和实际经验，我们知道电压-电流、电压平方-空载损耗是呈直线-三次趋向关系，而电压-功率是高阶曲线函数关系。很显然，我们只需要拟合出 
个试验数据点的这三条曲线的准确表达式来，上述问题就迎刃而解。对于电压-功率的高阶曲线函数关系，LabWindows/CVI函数库提供了 
个数据点的高阶曲线拟合函数PolyFit，只需要确定或选择阶数并代入有关数据即可。因此，我们需要解决的是直线-三次拟合曲线表达式的求取。
设分段函数 
曲线的连接点在 
处。
显然，上述曲线应满足以下条件：
（1） 
在 
处，俩式表达式值相等,有
（2） 在 
处，俩式斜率相等,有
 |
（3） 曲线要光滑，则斜率的变化率相等，即二阶倒数值相等，有
 |
根据上述关系，我们可以消去
， 
和 
，得出函数与 
， 
， 
的关系表达式。
并代入拟合曲线方程：
