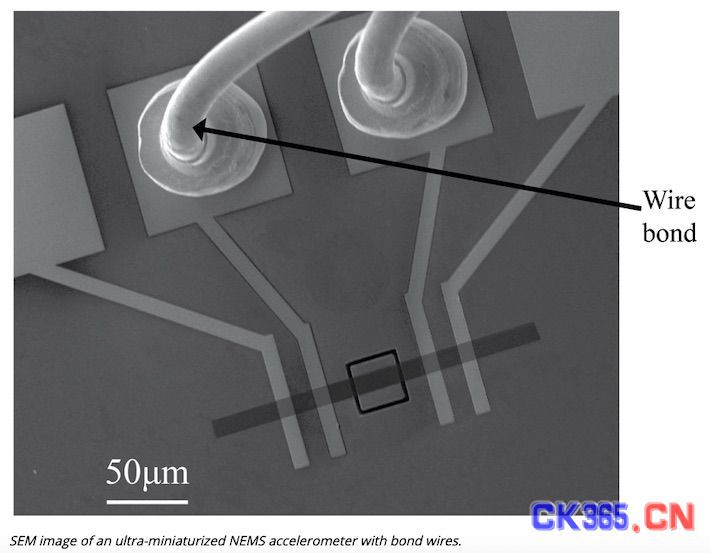
反激式转换器工作于电压模式控制(VM)的频率响应和在连续导电模式(CCM)下的驱动是次级命令系统。如果大多分析预示传递函数的品质因数只受各种损耗(欧姆路径、磁损耗、恢复时间相关损耗等)影响,那么由漏电感带来的阻尼效应非常小。但瞬态仿真预示输出阻尼随漏电感增加而振荡。由于现有文献中的公式没有反映出这影响,有必要采用新的模型,本文将作说明。
反激式转换器在CCM
一个理想的CCM反激式转换器在两个工作周期传输功率:
1)导通时间ton,在此期间初级端电源开关SW关闭,能量聚集在变压器初级电感Lp
2)在关断时间toff期间,开关打开,能量通过二极管D传递至次级端。然而,在检查原型波形时,可分辨出比基本解释描述更多的情况。图1显示一个采用变压器的典型的转换器受到漏电感lleak的影响。当电源开关关闭,在变压器初级电感Lp施加输入电压,开关欧姆损耗忽略不计。仔细看这原理图,这并不是精确的Vin,因为Lp和lleak分去了一部分电压。因而此时Lp的电压是
(1)

图1:反激式转换器工作状态显示当电源开关打开时,能量储存在初级端,随后能量在次级端循环
在ton期间并考虑到耦合点,次级端二极管被阻断。因为Lp和lleak串联,这些元件中的电流ip(t)循环增加,斜率为

(2)
当控制器指示开关打开,我们跳转到图(b)。此时感应电流发现集于漏极节点的电容中的一条通路。寄生参数由漏极端的MOSFET自身的非线性电容Crss和C oss ,加上钳位二极管的各种不同电容、变压器绕组间电容和反射到初级的输出二极管电容组成。所有这些元素集总为接地参考电容,定义为Clump。当电流流过Clump,漏源电压迅速增加。由于MOSFET的非线性电容,斜率是不恒定的。但我们可说这电压的斜率近似为
(3)
其中Ipeak是开关打开时的电流值。漏极电压增加,直到Lp电压反向。此时,如图1c,次级二极管偏置但次级端还没有电流流通。当Lp和lleak都通电,产生电流到持续充电的集总电容。由于是串联,Lp和lleak的电流相等,流过次级二极管的净电流为0。D开始导通的漏极电压为

(4)
输出电压现在反激到Lp——因而称为反激式转换器——并产生向下的斜率为
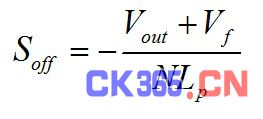
(5)
漏极节点继续增加,直到达到输入电压加钳位电平Vclp。此时钳位二极管导通,如图2a所示。当漏极节点电压保持在Vin + Vclp,漏电流不再流过Clump而仅为Vclp。集总电容的电荷吸收漏电感能量,现在Vclp中循环的电流略小于最初的峰值初级电流。
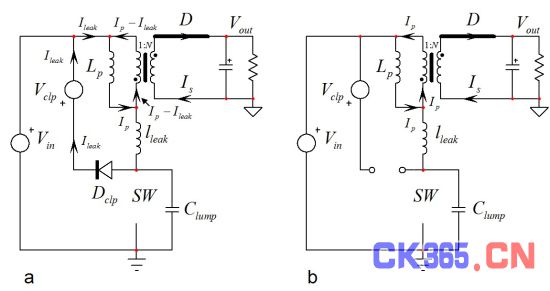
图2:当集总电容被充电到V in + Vclp,钳位二极管导通。
当开关打开具有峰值电流I p1 ,存储在电路中的总能量为

(6)
当钳位二极管开始导通,存储在集总电容中的能量为

(7)
此时,存储在电路中的能量现包括集总电容:
(8)
其中I p2 是集总电容充电后的循环电流。式(6)中的能量数不变,只不过其中一部分已传递到Clump。因而,
(9)
重新整理
(10)
从这一表达式中解得I p2 为
(11)
假定下列值
那么从(11)得出电流约976 mA或比打开开关时最初的1 A峰值电流减小2.4%。请注意,Clump是个高度非线性项,特别是在打开开关时的低电压点。如果(11)是个近似的理论公式,平台实验证实当二极管Dclp开始导通时在钳位网络中循环的电流更低。在漏极以额外的100-pF电容(1 kV用于离线应用)增加电容,将进一步减小电流。这额外的电容通过缓冲漏极电压有利于剩余电流装置(RCD)钳位温度和减小关断损耗。通过降低节点的dV/dt,EMI也将得以改善。但添加这电容可能会限制高线性导通损耗预算,如果开关频率很高。必须折中考虑。
在这点上,漏电感电压是固定的(忽略纹波):下部接线端保持在Vin + Vclp (忽略钳位二极管下降),而上部接线端为Vin +( Vout+Vf )/N。因而施加到漏电感的电压为Vclp-( Vout+Vf )/N 。漏电感的复位时间在此开始。(11)式定义的电流下降,斜率为
(12)
当漏电感复位,次级端二极管电流id (t)以(12)式定义的斜率产生,但此时为正并按匝数比增加。当漏电感完全耗尽,输出二极管电流达到峰值(图2b)。次级电流现在以(5)式定义的斜率减小。这下降斜率持续到开关再次打开。这是关断时间说明toff。但输出二极管电流不能立即返回到0。原因是需要时间激励漏电感:其电流必须跳转到初级电感仍然耦合到次级端。这是开关电流从0增加到谷底电流Iv的时间。当ISW = Iv,,所有初级电流现流过电源开关,次级端二极管阻断。从这些信息中可推断出两个重要要点:
1.当开关打开时,次级端二极管保持导通一段时间t1。这是漏电流从0增加到谷底电流Iv的时间。由于输出二极管在这较短的时间内一直导通,Lp退磁:漏电感延长次级二极管导通时间 。虽然开关关闭,初级电感斜率在漏电感电流达到谷底电流和整体流向地面前不会发生变化:占空比D减少d1。
2.当开关SW打开,次级二极管净电流为0,所有初级电流通过漏电感充电Clump分流。当漏电感复位,次级电流上升,并在复位完成时达到峰值:漏电感延迟次级电流产生的时间t2并影响其峰值。存储在漏电感中的能量加上初级电感的额外能量在钳位网络中被消耗。
这一事件的特写如图3所示。如您所见,漏电感明显延迟,并阻止次级电流立即达到峰值。而且,这峰值电流不是Ipeak/N ,而是如[1]所示为
(13)
图3:当漏电感被耗尽,次级端电流达到峰值。
更新Dc传递函数
现在我们对转换过程有了更好的理解,我们来计算已描述的小的时间事件t1和t2。t1是激励漏电感从0到谷底电流Iv所需的时间。当SW关闭,施加到漏电感的电压是反射输出电压(二极管D仍然导通)和输入电压Vin。忽略次级端二极管正向压降Vf,因而时间t1定义为:
(14)
如果我们规范化至开关周期,我们得到占空比d1为
(15)
漏电感复位时间t2以类似方式确定。当开关打开时(忽略集总电容充电时间),自D开始导通,施加到漏电感的电压是钳位电平减反射电压。因而我们有
(16)
一旦规范化至开关周期,我们得出占空比d2为
(17)
为确定转换器输出电压的一个好的工具是电感电荷平衡法,规定电感L在稳态时的平均电压是0:
(18)
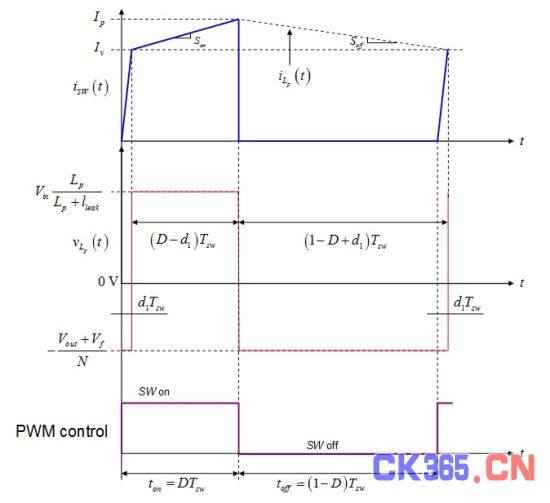
初级电感电压如图4所示。为符合(18),我们可写以下等式
(19)
在以上表达式中解得Vout并重新整理为
(20)
简化为
(21)
这时漏电感为0。
图4:初级电感稳态时的平均电压为0。
我们感兴趣的观察是有效的导通时间–在这期间,初级电感斜率为正–实际上是DTsw减少 。有效的占空比随着漏电感增加而进一步减小。施加到初级电感的电压也不是Vin ,而是更小,如式(1)。
简单的逐周期模型
为测试我们的计算和波形,我们已采集了一个简单的反激式转换器工作于40%的占空比,提供略高于60 W的功率。电气图如图5所示。漏电感已设为50 μH,如果您考虑600 μH的初级电感,说明变压器严重耦合(8.3%)。
图5:这简单模型仿真一个反激式转换器并展示其基本波形。
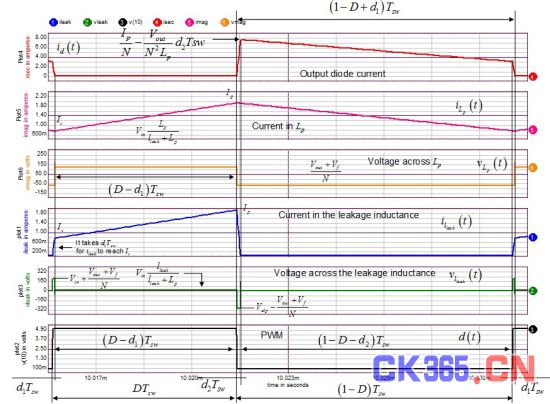
图6:这些波形显示我们在上文描述的所有事件。
通过仿真,我们可提取以下工作点,其中Vclp是C2两端的电压:
Ip=1.77A
Iv=672mA
Vclp=528V
漏电感磁化时间如(14)所描述,测量为176 ns。采用65-kHz开关频率,占空比d1为
(22)
理论上,变压器匝数比N为0.25,那么这反激式转换器的输出电压如(21)所定义,等于20 V。如果我们用(20),那么输出电压实际上应等于
(23)
仿真输出电压如图7所示并确定该值。请注意,我们在仿真中使用的二极管的正向压降为0 V。您可通过在二极管模型中设置扩散参数N为10m得到这结果。
图7:这些波形显示我们在上文描述的所有事件。
如果知道漏电感复位时间,还可精确计算输出电流。仿真提供的谷底电流为672 mA,而峰值电流为1.77 A。应用(16)和考虑528 V钳位电压(图5中 C2两端的电压),漏电感复位时间为
(24)
相对应的占空比为
(25)
我们还可预估在开关关闭后193 ns,漏电感复位时的次级峰值电流。应用(13),我们发现
(26)
从图3的低边波形,我们现可通过计算构成该曲线的各个不同领域确定在二极管和负载中循环的平均电流:
(27)
导入数值,我们有
(28)
这是由波形观测仪给出的值,如图8所示。
图8:仿真次级端平均电流取决于峰值和各种小占空比d1和d2。
硬件验证
为证实我们的分析,我们已建立了简单的固定占空比反激式转换器,其漏电感已被人为地增长到初级电感的2.5%,通过增添一个外部电感。图9显示MOSFET漏极电压和次级端二极管电流。正如预期,当开关打开时,次级电流没有立即增加。这是由漏电感退磁时间引起的延迟。在图右侧,您看二极管波形略微落后于急剧下降的漏极电压。这是漏电感从0到谷底电流的磁化时间。图10 的特写证实了62 ns的导通时间。MOSFET的导通与下降的vDS (t)很好地同步,但Lp的磁化周期在62 ns后才真正开始。在这62 ns期间, Lp保持退磁,虽然MOSFET已导通。这现象在这里非常短暂,显然可忽略不计。但您可清楚地观察到延迟,这将获得显著更长的有源钳位架构。
图9:采集的原型波形显示次级端延迟,但小的次级二极管导通时间也延长。
图10:下降沿的特写显示次级端二极管延迟62 ns
在图11中,您可清楚地看到次级端电流延迟,但您也可计算漏电感复位时间。在此期间,在开关打开后,漏极电压达到稳定值。在本例中这时间持续217 ns。超调量相当重要,并取决于钳位二极管正向传输时间。必须在评估MOSFET 漏源击穿电压(BVDSS)的最余差量时考虑到。当RCD二极管被堵塞,高频振铃涉及漏电感, Clump产生。阻尼这些振荡有时是必要的,因为它们可严重辐射和影响EMI信号。确保涉及RCD钳位的回路极短并靠近变压器。将几十欧姆的电阻与二极管串联有助于阻尼这些振荡。
图11:观察漏极电压显示所需的信息,特别是漏电感复位时间。
在这示波器截图中,延迟持续很短的时间,因为漏电感迅速复位。但在有源钳位转换器中,涉及lleak和Cclamp的谐振在关断时发生,自然延长复位时间。这谐振在次级产生平滑断续的波形,即使工作在CCM模式。
结论
这第一部分显示反激式转换器波形受到漏电感的影响。有效的占空比减少了激励漏电感所需的时间,而初级电感退磁延长相同的时间。Dc转换器功能受到影响,并得出新的表达式。这些事件在反激式转换器中是微小的,难以想象与一个良好耦合的变压器联系在一起。但在有源钳位转换器中,这时间可能是显著的。我们第二部分将重点讨论由漏电感带来的小信号效应。