1、问题背景: 主动配电网中的不确定性因素给恢复控制带来了挑战
1.1配电网恢复控制原理
配电网通常呈辐射状运行,当电网发生故障时,将导致故障点所在线路的下游区域全部停电。配电网中的开关一般分为常闭的分段开关和常开的联络开关两类,对故障进行定位与隔离后,可通过协调这两类开关的开合状态,将非故障停电区的负荷转接到其他馈线或同一馈线的带电支路上,实现供电恢复。因此,恢复控制本质上是一个满足配电网运行约束下的开关组合优化问题。
1.2主动配电网中的不确定性
由于许多设备的操作需要人工执行, 实际的供电恢复是一个耗时过程,期间存在的不确定性因素主要有:
1) 分布式电源出力波动:以光伏和风电为代表的分布式电源(DG)的出力,会受天气和环境因素的影响而发生波动。随着分布式电源在配电网中渗透率的不断提高,其出力不确定性对恢复控制的影响将日益显著。
2)节点负荷波动:节点负荷值取决于用户用电情况,是一个无法精确预测的时变量。
3) 负荷估计误差:由于目前配电网安装的负荷量测装置很少,大部分非量测节点只能通过典型负荷曲线法或短期负荷预测法获得伪量测数据,因此其估计值与真实的负荷值之间可能存在较大偏差。
1.3传统确定性算法存在的问题
在传统的恢复控制算法中,分布式电源出力和负荷均用单点预测值表示, 视为确定性参数,这种确定决策模型存在安全隐患。例如,倘若恢复期间实际的负荷高于预测值,分布式电源出力低于预测值,由确定性算法生成的恢复策略可能造成线路过载或电压越限,最终导致供电恢复失败。因此,主动配电网中的不确定性因素给传统的确定性算法带来了挑战。本文提出一种新的鲁棒恢复控制方法, 使得产生的恢复策略在这些不确定性参数(分布式电源出力、负荷波动和估计误差)在给定的范围波动时,供电恢复方案总是能保证电网安全的,即可行的。
2、算法模型: 保守性可调的鲁棒恢复控制优化模型
常见的确定性建模方法可以分为随机模型和鲁棒模型,但是随机模型需要给定变量概率分布,而且存在计算困难问题。为此,本文对配电网恢复控制决策问题构建为一种两阶段鲁棒优化方法问题,包含以下几个步骤:
步骤1:将一般的恢复控制决策描述为一个混合整数线性规划模型,其目标函数为最大化恢复失电负荷,约束条件包括辐射状拓扑约束、功率平衡约束、线路容量约束和节点电压安全约束等。该模型暂不考虑不确定性因素,是一个确定性恢复控制优化模型(DROM)。
步骤2: 根据历史数据,构建出分布式电源出力和负荷的不确定性区间。
步骤3:基于DROM和不确定性区间,建立两阶段的鲁棒恢复控制优化模型(RROM); 其第一阶段为生成最优的失电负荷恢复策略,第二阶段是在不确定性区间中搜索出最恶劣的波动场景。
步骤4:引入不确定性预算(Budget of Uncertainty)技术调节该模型模型保守度, 使得该方法能够在鲁棒性和保守性中做权衡。
最终,考虑分布式电源出力不确定性和负荷不确定性的恢复控制决策,被建立为保守度可调的两阶段鲁棒优化模型。针对这样的两阶段问题,本文使用列约束生成法将其分解为主问题和子问题进行迭代求解。由该模型生成的恢复策略,对于不确定性区间中的所有波动场景均能保证不出现配电网运行约束被破坏的情况。
3、算例验证
采用PG&E 69节点配电系统进行算例验证,通过最恶劣波动场景测试和蒙特卡洛仿真,对比分析确定性模型DROM和鲁棒模型RROM的恢复控制效果。
1) 最恶劣波动场景测试
对整个算例测试系统进行一次“N-1”故障扫描, 提取出子问题中生成的最恶劣波动场景作为测试环境。确定性模型和鲁棒模型的故障恢复情况如图1所示:红色表示的确定性模型在最恶劣场景下出现了多次恢复失败的情况,需要额外切除部分负荷(恢复负荷量取负值)才使得恢复策略可行;而蓝色表示的鲁棒方法在所有线路故障的情况下均保证了决策的可行性和优化性。
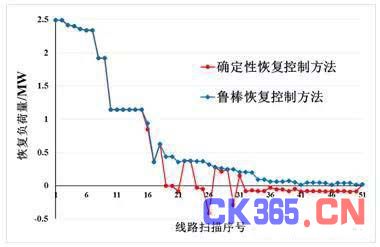
图1 PG&E 69节点系统的“N-1”扫描结果
2) 蒙特卡洛仿真测试
设实际的分布式电源出力和节点负荷是呈以预测值为中心的正态分布,并对每个故障情况随机生成3000个波动场景作为测试场景。四个典型线路故障案例的负荷恢复情况如表1所示,其中鲁棒方法一直保持着100%的恢复成功率和最优的恢复负荷量,而确定性方法在不少场景下会出现恢复性能不佳,甚至恢复失败的情况。
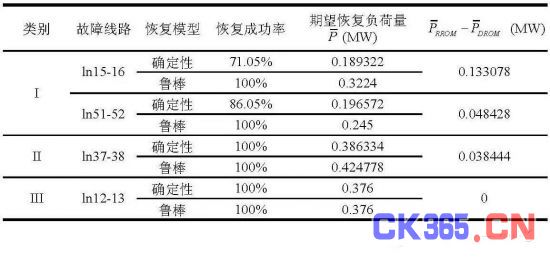
4、结语
本文提出了一个保守度可调的两阶段鲁棒恢复控制优化模型,建立为混合整数线性规划的形式。基于给定的不确定性区间,该鲁棒模型能够搜索出最恶劣的波动场景,并进行恢复控制策略的生成。算例结果验证了本文方法的鲁棒性和优化性;该方法可用于解决恢复过程中由于分布式电源出力波动、负荷变化以及负荷量测误差大造成的恢复控制策略不可行问题。