一、研究背景
在微波暗室内对基站天线进行测试是一种常用的方法。由于暗室尺寸的限制,对增益较高的天线,往往不能满足远场测试条件。在这种情况下测试结果与远场情况下的测试结果有较大差异。本报告给出了一种由准远场距离上测得的方向图计算远场方向图的方法。
二、修正算法的基本原理
如图1所示的AUT为基站天线,天线沿着y轴方向的尺寸较小,容易满足远场条件,而x方向的尺寸较大,不满足远场条件。针对这类天线的方向图,可以采用该方法进行修正。
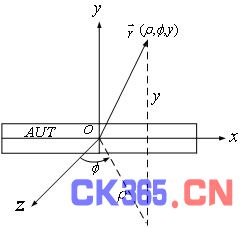
图1 天线坐标系
以oy为轴作一个能完全包围待测天线的最小柱面,设该柱面的半径为rmin。在该柱面之外,天线产生的电场可表示成矢量波函数
令场点位于xoz平面(即y=0),且ρ较大时,式(1)可以表示为
其中:Nm=krmin+10
由于场点(ρ,φ,0)已经处于天线的准远区,且ρ相对于天线的垂直尺寸(y轴方向)已经很大了,对上式中的积分可以采用一维驻相法进行计算,并考虑到
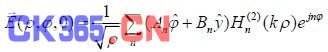
对于任意的线极化电场分量均可以表示为

如果在ρ=ρo处测得电场为Em,则有

可以求出
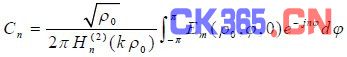
将Cn代入公式(5),命ρ→∞,则得到天线远场为
其中,C为与角度无关的常数,可以略去。天线的远场方向图为
基于以上关系式,容易得到远场条件下天线增益与准远场条件下增益的差值为
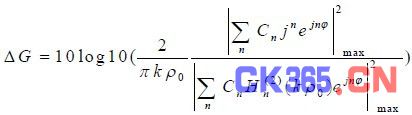
三、数值仿真验证
为了验证该算法的正确性,进行数值仿真验证。选取一个工作频率为900MHz,口径为2.6m的阵列天线进行数值仿真分析,准远场测试距离为29m(该测试距离不满足远场条件)。数值仿真流程和数值仿真结果分别如图2和图3所示。
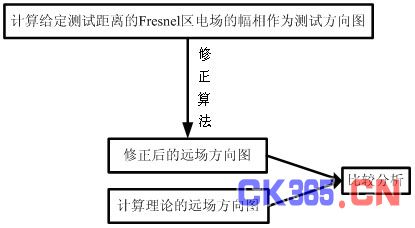
图2 数值仿真流程图
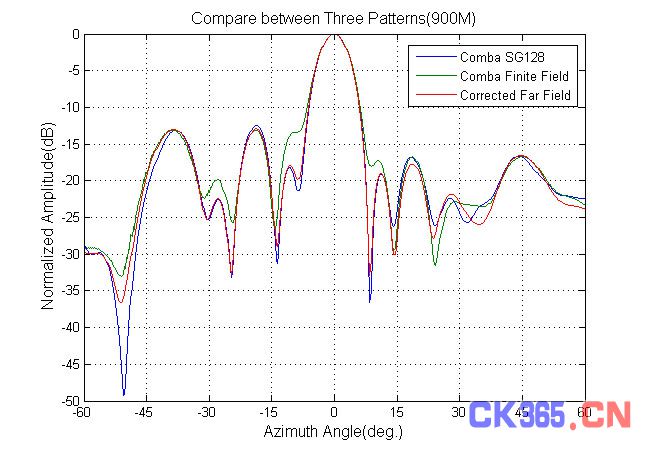
图3 数值仿真结果
由图3可知,测试结果(Measured Pattern)与理论结果(Theoretic Pattern)差别较大,修正后的结果(Corected Pattern)与理论结果(Theoretic Pattern)吻合很好。
四、实验验证
为了验证以上算法的正确性,对给定的天线分别按如下两种方法测试:准远场测试和球面近场测试。通过修正算法对准远场测试结果进行修正,并将修正得到的远场方向图与球面近场得到的方向图进行对比,结果如图4所示。

图4 实验结果与修正结果
图4可知,准远场测试结果(Comba Finite Field)与球面近场测试结果(Comba SG128)有较大差距,修正结果(Corrected Far Field)与球面近场测试结果(Comba SG128)吻合良好。
五、结论
经过数值仿真分析和实验测试证明了上述算法的可行性与准确性。



