前言
振弦式传感器是基于钢弦频率随钢丝张力变化而变化的原理工作的,具有结构简单、精度高、长期稳定性好等优点,输出为频率信号,有较强的抗干扰能力,便于长距离传输。因此,振弦式传感器被大量应用于建筑、水利工程、铁道交通、冶金、煤炭等部门,可用于应力应变、变形、渗流、液位、温度等自动化测量[1]。
分析振弦式传感器的工况可知,温度是影响其测量精度的重要因素之一,因此温度补偿效果的好坏直接影响着振弦式传感器测量精度的高低。温度补偿可分为硬件补偿和软件补偿。由于硬件补偿法难以实现高精度的补偿且存在漂移问题,因此利用人工神经网络的软件方法对传感器信号进行温度补偿。神经网络具有良好的自学习、自适应和非线性映射能力。其中BP网络是目前应用最多的一种前馈网络,但BP网络存在收敛速度慢、容易陷入局部最小值等缺点。
针对上述问题,作者提出利用优化的BP网络———LMBP网络建立振弦传感器温度补偿模型,来提高传感器测量的精度和稳定性。
1 振弦传感器工作原理

非膜式振弦传感器一般由固定支座、激振线圈、钢弦等部分组成。可等效为两端固定绷紧的均匀弦,单线圈传感器的等效物理模型如图1所示。
两端固定且拉紧的振弦的固有频率f0的表达式
式中:f0为弦的基频; l为弦的有效长度; T为弦所受应力;ρ为弦材料的线密度。
对一个完工的振弦式传感器,其线密度ρ确定,若忽略有效长度l的变化,则只要测得弦的振动频率f就可以计算得到待测物理量T[2]。
2 基于LMBP神经网络的振弦传感器温度补偿
BP算法由信息的正向传递与误差的反向传递两部分组成。在正向传递过程中,输入信息从输入层经隐层逐层计算,传向输出层,每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有得到期望的输出,则计算输出层的误差变化值,然后转向反向传递,通过网络将误差信号沿原来的通路反传回来,修改各层神经元的权值直至达到期望目标。
2·1 LM算法
BP网络体现了前向网络最精华的部分。但是传统的BP网络存在收敛速度慢、容易陷入局部最小值等缺点。作者以传统BP网络为基础,利用Levenberg-Marquardt (简称LM)算法优化计算BP权值和阈值修正量。LM算法将梯度下降法和高斯-牛顿法相结合,实现了收敛速度与稳定性的统一。下面简要介绍LM算法[3]:
设wt表示第t次迭代的权值,则修正后的wt+1次权值可用下式表示:

LMBP神经网络克服了传统BP网络的缺点,极大地提高了收敛速度,同时保证了精度和稳定性。
2·2 网络训练样本的建立

神经网络法不必建立包括待消除的非目标参量在内的函数解析式,而只需要训练样本,通过学习、训练便可以模拟出输入输出的内在联系。所以只用通过实验来得到样本数据则可用于网络训练。文中的目的是要补偿掉温度对振弦式传感器的影响,所以除了知道传感器受压时的频率值f以外,还应该有相应的表示温度值的数据,原理框图如图2所示。
在实验中,选用Geokon 4500S-50型振弦式传感器,当标准压力p=3 820·670 6Pa时,将温度从15℃逐一升到30℃,得到对应的压力和频率输出值,如表1所示。
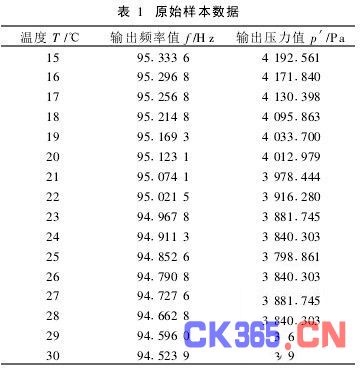
从表1可以看出,相同的标准压力在不同的温度环境下,传感器的输出压力值p′相对标准压力p最大偏差达到371·890 4Pa,必须对温度进行补偿。
受BP神经网络传递函数作用范围的限制,应将样本数据进行归一化处理。考虑到LMBP算法应用的传递函数为Sigmoid类函数,该函数在自变量处于饱和区时,收敛速度慢。因此将输入与输出数据变换在[0·05~0·95]之间,这样Sigmoid类函数在该区间内变化梯度增大,网络收敛速度快,网络性能改善。
具体算式为]

式中:X归一为网络的输入、输出归一化后的值; Xi为样本第i个输入、输出值; Xmax、Xmin分别为样本的最大、最小值。
将温度T和频率f的值归一化后作为网络的输入,标准压力p归一为0·05后作为网络的输出值即目标向量。
2·3 隐层节点数的确定及网络训练
根据BP网络的Kolmogorov定理:对于任何在闭区间内的一个连续函数都可以用单隐层的BP网络逼近。所以采用单隐层的3层BP网络。
隐层节点数的确定是网络的一个关键部分。到目前为止最佳隐层节点数的选择没有一个固定的公式,可以用公式N=n+m+a (n, m为输入输出节点数, a=1~10)来初步估计。初步设定隐层节点数范围为5—17,在MATLAB里编写一个隐层节点数可变的程序,最后确定节点数为15时误差最小[5]。
隐层传递函数选用S型正切函数tansig,输出层神经元的传递函数采用S型对数函数purelin。网络最大训练次数设为2 000次;误差平方和指标定为0·000 01;网络的训练方法选用trainlm,它是专门用于LMBP网络的训练函数,它包括了计算雅克比和赫森矩阵的功能。
2·4 网络训练结果
网络训练的运行结果如图3所示,从图中可见,利用trainlm训练网络,仅8次训练就达到了最小梯度。此时的训练误差为2·954 4×10-7,已经达到目标误差10-5,说明此网络性能满足要求。网络训练的输出向量与目标向量的误差曲线如图4所示,由图可见,输出向量与目标向量的误差已达到10-4,已经能满足性能要求[6]。

反归一化后的压力计算值p″如表2所示。
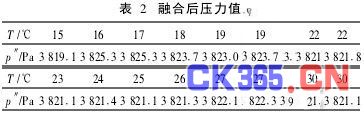
融合前。由表1可以看到,随温度变化测得压力值p′相对标准压力值p的最大偏差为371·890 4Pa,压力值最大相对波动为
融合后。由表2可以看到,随温度变化计算得压力值p″相对标准压力值p的最大偏差为4·629 4Pa。压力值最大相对波动为
3 结论
通过分析温度对振弦式传感器的影响以及对传统BP神经网络的缺点分析,说明了LMBP神经网络对消除传感器在工作过程中受温度干扰的影响十分有效。采用LMBP神经网络对现场实际测得的数据进行融合处理,处理后的最大相对波动减少为0·12%,避免了网络陷入局部极小值,大大减小了网络的训练次数,提高了收敛速度。
综上所述,可知LMBP神经网络是一种有效的数据融合处理方法,对振弦式传感器能够进行很好的温度补偿,具有一定的工程应用价值。






