1 引 言
智能材料必须具备感知、驱动和控制这3个基本要素。其中“感知”要素是最基本的要素,是实现“驱动”和“控制”要素的基本条件,“驱动”和“控 制”是智能材料的目的。所谓的智能材料和结构的自诊断功能,是指结构能够根据外界环境变化引起的材料响应判断导致该响应的起因,并对结构自身反应及反应的 累积历史进行评估,对未来使用情况进行一定的预测。这个识别、评估、预测的过程,实质上是对检测数据的智能计算和处理过程,可归结为力学上的反分析问题 [1]。
通常智能结构感知的信息是离散的、有限的,而且不可避免地含有一些误差,如何由这些有限的、含有误差的信息推断出起因便是自诊断功能要完成的任 务。本文将探讨根据埋入复合材料或粘贴在材料表面的传感器所提供的材料上若干个点的应变来识别同时加载在板结构试件的多个静态集中载荷的大小和位置的算 法。
2 基于遗传算法的载荷识别原理
目前常用的载荷参数识别方法有:采用正则化方法和最小二乘法识别板结构受载后集中力的大小和位置[2],采用最小二乘法和边界元方法或有限元方 法结合研究二维弹性反问题[3, 4],人工神经网络的方法[5]等。这些方法通常只用于识别单个集中载荷,无法识别多个集中载荷。因此必须寻找一个新的算法来解决载荷识别问题。
2·1 多载荷识别存在的难点
逆问题分析存在解非唯一,是多载荷识别的最大难题。这是因为通常埋入板结构的传感器是点传感器,而非分布式传感器。受成本限制和设备处理能力的 影响,传感器的数量不可能太多。这样不同的载荷组合就有可能有相同的传感器值,造成误识别。所以,要想获得唯一的解是不现实的,所识别的结果应是最优解。
另外,对于神经网络这类需要训练样本的算法,样本的数量也是一个重要考虑因素。为了防止神经网络出现欠学习现象,样本的数量必需足够多。在 300×300的板上用神经网络进行单个载荷识别实验,在板面上划分100(10×10)样本点,每个点分别施加10次大小不同的载荷,则样本量为 1000个。经过训练后,神经网络能较好地识别单个集中载荷。若要识别多个载荷,仅以两个载荷识别为例子,在不同样本点上的载荷两两组合就可能达到近百 万。这就意味着使用该算法所需要的训练工作量太大,致使算法无法实现。
对于神经网络,多载荷识别还有另外一个难题,就是神经网络结构的确定。由于事先不知道施加在试件上的载荷数量,因此神经网络输出的节点数就无法 确定,以至于整个神经网络的结构就无法确定。由于每个载荷的参数有3个,力的大小和坐标(F、X、Y),要识别n个载荷所需要的输出节点就要3n。输入节 点由传感器数量决定,而传感器数量不可能太多,所以,用于多个载荷识别的神经网络有可能出现输出节点的数量大于输入节点。这样的网络结构是不合理的,不容 易收敛。因此,我们称神经网络不方便用于“表达”多载荷识别问题。
从上述可以看出要实现多载荷识别必须解决以下3个问题:最优解、所需训练样本数量太多以及算法是否方便用于“表达”多载荷识别问题。
2·2 多载荷识别算法思路
由于逆问题的分析会出现的不适定的难点,尤其是对于多峰值问题,无论是采用常规的优化算法或是人工神经网络的方法,均存在收敛性差和仅收敛于局 部非劣解的缺点,使得逆分析达不到精度要求。近几年来,开始将遗传算法(GeneticAlgorithm)用于优化和逆分析。它按照生物的遗传特点,通 过遗传因子的信息传递、变异及自然淘汰,使得可在大范围域内对可行解进行并行探索。从而对多峰值问题,可得到全域的优化解,避免仅得局部非劣解的弊病。遗 传算法对离散型的设计(识别)参数,尤其显得实用、有效[6]。本文介绍的算法以遗传算法为核心,思路如下:①通过相关分析方法来实现对载荷数量的识 别;②在已知同时加载在板结构试件的载荷数量的情况下,可以使用遗传算法求解载荷的所有载荷的大小和位置。
2·3 相关分析方法简介
算法原理如下:
在试件上划分m×n个网格,每个网格称为样本点。在一个样本点上加载,读取分布在试件上的所有传感器应变数据,并把这些数据组成一个向量,然后 对该向量进行规一化处理。即,求由分布在试件上的传感器应变数据组成的向量的单位向量,该单位向量是一常量,与载荷大小无关,仅由加载点位置决定,称为该 样本点的“受载模式”,简称“模式”。它反映了一个点受到载荷后,各个传感器应变数据之间的关系。对所有样本点进行加载,获得所有样本点的模式,称为已知 模式。
待识别数据也进行规一化处理,称为待识别模式。然后待识别模式与所有样本点已知模式的皮尔逊(Pearson)相关系数,并按样本点的位置顺序排列,组成一个二维相关系数矩阵。待识别模式w与样本点(i,j)模式mij的皮尔逊相关系数ρ如式(1):

图1、图2、图3显示(0·2 m,0·2 m,500 N)、(0·2 m,0·8 m,500 N)、(0·8 m,0·8 m,500 N)3个载荷分别单独加载在板结构上时的相关系数矩阵三维图形。单个载荷加载时,矩阵只有一个正峰值点。研究发现:多个载荷同时作用时,待识别模式与所有 已知模式的相关系数矩阵是每个载荷单独作用相关系数矩阵的线性组合,推导如下。
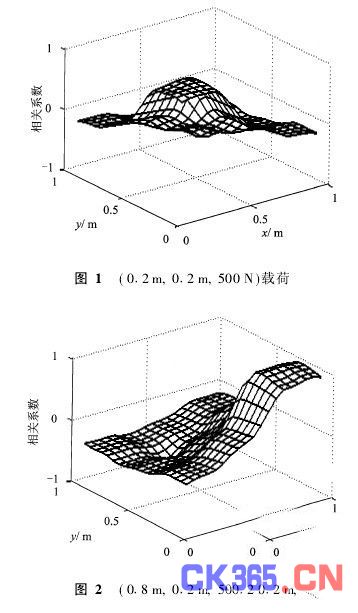
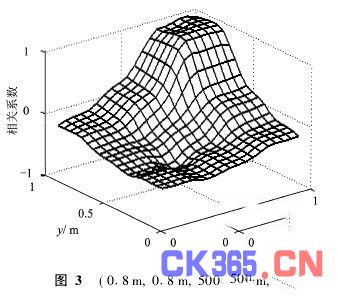
S1、S2、S3为3个载荷单独作用时的传感器应变数据向量,S为3个载荷同时作用时的传感器应变数据向量(假设所有载荷都加载在样本点上),根据叠加原理有:

式中,D、D1、D2、D3分别为w、x、y、z与所有样本点模式的相关系数矩阵。
因此,矩阵中的正极值点个数就是试件所受到的集中载荷数,每个极值点所对应的位置附近有其中的一个载荷。如图4所示(0·2 m, 0·2 m, 500N)、(0·2m, 0·8m, 500N)、(0·8m, 0·8m, 500N)3个载荷同时作用在试件上,所以相关系数矩阵有3个正峰值。
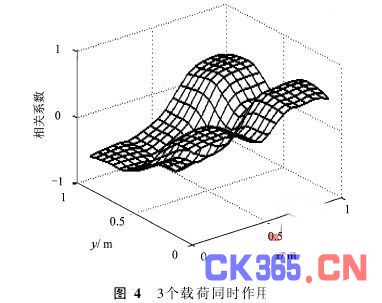
在载荷数量已知情况下,可以用遗传算法求解载荷的参数。
2·4 基于遗传算法的单载荷识别
用遗传算法根据应变值求解外载荷实际上是依概率搜索最优解的过程。为了更好地描述算法,本文先叙述基于遗传算法的单个载荷识别方法。
2·4·1 编码
对外载荷(包括力的大小、X、Y坐标)用一维的二进制进行编码。由于传感器测得的应变值对载荷位置较敏感,即载荷位置有很小的偏差将引起传感器 读数产生较大的变化,位置推测的一点小误差会引起载荷推测的大误差。所以对载荷位置(X、Y坐标)应有较长的编码,以减少量化误差,使得遗传算法能得到比 较精确的结果,否则算法收敛的结果将有较大的误差。
2·4·2 初始种群
初始种群由随机函数产生。初始种群的数量应根据解空间的大小来确定。太大则算法的计算量大,耗时太多。太小又使进化缓慢造成代数增加,而且可能产生早熟现象而得不到理想的解。
2·4·3 适应度函数
适应度函数用于评价种群对环境适应程度。遗传算法对适应度函数没有要求,可以使用非连续、不可微或隐式函数,还可以神经网络作为它的适应度函数。
本课题的适应度函数用来评价种群(载荷)所能产生的传感器处应变与实际测量值的接近程度。构造适应度函数如下:
载荷与传感器应变值的映射关系
这是一个正解问题。其中P是载荷参数(载荷大小f,加载点位置坐标X,加载点位置坐标Y);S是该载荷所产生的多个传感器应变向量。通常函数F 可以用有限元来实现。但是有限元模型存在不容易建立以及建立后的模型与实际试件之间是否一致,有限元计算量太大等问题。本课题决定使用神经网络来替代有限 元分析。即在试件不同位置施加不同载荷,把载荷的大小和位置作为神经网络的输入,在该载荷下测量的应变值作为输出,对神经网络进行训练。利用神经网络的泛 化功能来推测载荷的输出[7]。载荷数量少的情况下,会出现输出节点数大于输入节点数。为了能使神经网络能收敛,实验采用多个神经网络并联的方法,每个神 经网络的输入是所有载荷的参数,输出其中一个传感器数值。有多少个传感器就要有多少个神经网络。
④种群中每个个体(载荷)所能产生的传感器处应变S与实际测量的值S0几何距离:
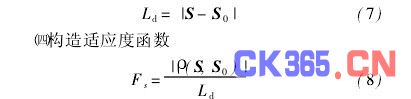
用S和S0的相关系数以及几何距离的倒数来构造适应度函数,满足遗传算法适应度函数的要求:必须是正值;误差越小,适应度值越大。
2·4·4 模拟结果
该方法使用有限元提供的数据进行测试,能获得满意结果。
使用有限元软件建立一个1 m2四边固支的正方形平板,指定均布的9个点的输出作为传感器输出。再找出均布的25个点,每个施加0到1 000 N的压力(间隔50 N),这样共有1 000组数据对神经网络进行训练。
对每个传感器建立一个BP神经网络,输入层节点数为3,中间层为10,输出层为1。这样每个神经网络可以计算一个载荷对该传感器的影响。
用P(320 N, 0·35 m, 0·35 m)作为测试载荷进行测试。编码长度11,初始种群200。经过5到7代后得到的结果如下表1。
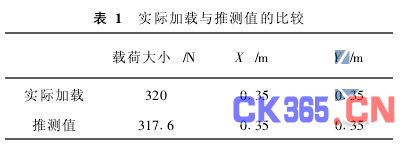
载荷P的应变值(由有限元软件提供)与神经网络计算的应变值比较如表2。

2·4·5 多个载荷识别
遗传算法提供了计算两个以上载荷的可能性。对多个载荷,只要对上述遗传算法稍微加以修改就可以。
首先,编码应是可变长度的,若判别一个载荷的编码长度是11位,则n个载荷编码就是11n。每11位就是其中一个载荷的参数。其次,在适应度计 算中,可以对每个载荷应用神经网络,获得单个载荷传感器值。然后利用力的叠加原理,把这些传感器值相加就获得多个载荷与传感器示值之间关系的表达。这种算 法只需要单个载荷的数据作为样本就可以了,无需获得多个载荷同时作用的数据,大大减少训练工作量。
在已知图4所示的3个载荷同时作用下传感器值和载荷数量情况下,使用遗传算法得到3个载荷的解分别为:(0·2 m, 0·3 m, 370 N)、(0·8 m, 0·2m, 490 N)、(0·8 m, 0·8 m, 450 N)。使用遗传算法求解载荷参数的精度除了与编码的长度有关,还与适应度函数的神经网络精度有关。
2·5 算法特性
由于在遗传算法的适应度函数采用神经网络,因此本课题的技术方案甚至设备和程序基本不必修改就可以用于其它材料和试件,具有良好的推广性。
④遗传算法有一定的数据融合能力。
在对国产某型飞机的机翼盒段上进行实验时发现,使用遗传算法载荷识别精度较神经网络高。经过分析,这是由于在遗传算法中适应度函数应用了个体 (载荷)所能产生的传感器处应变S与实际测量的值S0几何距离的倒数的缘故。由于适应度函数中使用了几何距离,使得遗传算法具有一定的数据融合功能。
实验时,为了在盒段面板的背面埋入光纤传感器,必须把面板卸下,埋入传感器后重新装上。由于实验室条件的限制,面板的安装精度不能保证,安装后 有残余应力存在,造成测量数据误差较大。在同一个样本点两次加载,某些传感器值(尤其是应变值较大的)有可能相差15%~20%。在这种情况下使用神经网 络进行载荷识别是不可能达到精确的。这是因为训练样本的数据与实测数据不一致。根据模式概念,在一个点加载时,各个传感器数值之间是有一定关系的,不是任 何一组数据都可以构成传感器的应变值。由于残余应力的存在,测试载荷的传感器数据可能不符合样本数据的特征。使用神经网络是不一定能解出精确的载荷,甚至 会出现不合理的解。
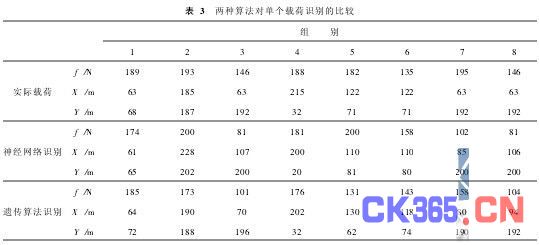
把样本的传感器数据向量空间称为定义域,则其所对应的载荷就称为解空间。直接用神经网络求载荷,若实测数据不在定义域内,则所求得的载荷就可能 不在解空间内。有可能出现载荷位置超出试件大小等不合理解。在遗传算法中,神经网络是用于代替有限元软件,用于求解正问题的,即输入载荷求传感器数据。由 于这些神经网络是用样本数据训练的,所以它所解出的传感器数据与样本数据是一致的。遗传算法的编码方式决定了它的解只能在解空间中,即遗传算法是在解空间 中搜索最优解的。所谓的最优解就是该载荷所引起的传感器应变向量(一定在样本空间所决定的定义域内,由神经网络求解)与实测载荷的传感器向量几何距离最 小。这样即使实测载荷的传感器向量不在定义域内,也能获得相对较为精确的解。表3为两种算法对单个载荷识别的比较,可以看出使用遗传算法精度更高。
(四)有冗余能力
遗传算法有一定的冗余能力。当某些传感器失效时,算法应能保证系统在性能略为降低的情况下继续工作。在上述的遗传算法中,用于求解的神经网络数 量与传感器数量一致,当某个传感器失效后,只要停止其相对应的神经网络的工作,并不影响算法的实施。本算法最少需要4个传感器。
传感器布局
光纤布喇格光栅传感器只能测量单个方向的应变,为了提高载荷两个方向位置的识别精度,必须进行两个方向的应变测量,若只用4个传感器,则可以考虑沿着面板对角线布置,可同时兼顾两个方向的应变测量。



