0 引言
大型天文望远镜在跟踪星体目标时运动速度非常低,同时要求望远镜具有很高的速度平稳性,因此,要求其伺服控制系统能进行实时准确的速度测量。由于目前角速率传感元件零位位置、零位噪声的制约,常采用位置型测量元件光电编码器来测量速度,一种最直接的方法就是在一个采样周期内,用位置测量值的一阶后向差分来估计系统的瞬时速度[1],由于光电编码器量化误差以及测量噪声的存在[2],当速度较低且采样周期较小时,差分算法会放大编码器输出的随机误差成分,明显降低低速测量精度。
提高编码器分辨率固然可以改善低速测量精度,但这无疑会增加测试成本,目前,在编码器分辨率一定的情况下, 解决其低速测量问题的主要方法有两种:第一种为硬件处理方法, 诸如针对M 法、T 法测速的不足,相继提出M/T 法测速[3]、变M/T 法测速[4]以及双缓冲法[5],这些方法的共同特点是需要码盘脉冲信号的上升沿或下降沿来同步时间信号, 因此,需要额外的硬件电路支持,另外,它们只适用于增量式编码器,不适用于绝对式编码器;第二种为软件处理方法,即通过对编码器输出角度进行滤波或者预测等方式,改善编码器的低速特性。如参考文献[6]提出采用滑动窗多项式拟合模型,结合最小二乘递推算法来提高轴角编码器的测角精度, 进而提高差分测速精度,由于这种方法使用滑动窗口滤波技术,很难保证实时性的要求,另外,使用卡尔曼预测滤波技术[7]、状态观测器[8]来估计速度信息的方法也得到了应用,然而, 这两种方法都需要建立对象模型来提取状态信息,而实际系统模型参数并不能精确测量得到。
针对上述问题,文中将非线性跟踪微分器理论应用于轴角编码器测速,提出了一种仅基于位置测量的速度估计方法。它不基于对象模型,可以从受到噪声污染的信号中快速有效地估计出输入信号及其微分信号,由于用积分方式代替微分方式,避免了常规差分算法带来的噪声放大问题,另外,该方法只利用以固定周期采样的位置信息,因此,既适用于增量式编码器,也适用于绝对式编码器。文中将这种方法应用于光电望远镜系统的轴角编码器测速,明显提高了低速测量的实时性和准确性,进一步将此方法应用于速度闭环反馈控制,也改善了低速跟踪的速度平稳性。
1 理论
非线性跟踪微分器(NTD)最初由中国科学院韩京清研究员提出,主要用于解决在不连续或带随机噪声的量测信号中,合理地提取连续信号及微分信号的问题。它克服了经典的差分求微分算法的弊端,对噪声有较强的抑制能力。非线性跟踪微分器的结构如下:对它输入一个信号r(t),它将给出两个输出变量x1 (t)和x2 (t),其中x1 (t)始终跟踪r(t)的变化,而x2 (t)则是x1(t)的微分信号,当x1 (t)快速跟踪r(t)时,x2 (t)便可作为r(t)的近似微分[9]。构造跟踪微分器的理论依据如下:定理若系统(1) 的任意解满足z1 (t)→0、z2 (t)→0(t→∞)

定理表明:选择恰当的非线性函数f(·), 使系统渐近稳定,则系统状态x1 (t)平均收敛于输入信号r(t)。由于x2 =x1 ,则x1 (t)弱收敛于r(t)的广义导数r觶 (t),即状态x1和x2分别跟踪输入信号及其微分。参考文献[9]对此问题给出了严格的数学证明。由于x1和x2均可通过输入信号r(t)的积分运算得到,避免了常规差分算法带来的噪声放大问题。在数值计算时,
为了避免平衡点附近产生的振颤现象,实际使用时常采用基于欧拉方法离散化的微分跟踪器[10],如下所示:
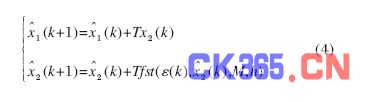
式中:T 为采样时间;ε (k)=x赞 1 (k)-r(k), 为输入变量r的估计误差;M 为速度因子,主要影响跟踪速度;h 为滤波因子,主要影响滤波效果。非线性函数fst(v1 ,v2 ,M,h)定义如下:

可以看出:离散NTD 具有算法简便、计算量小的特点,便于实现角速度的实时测量;另外,只有两个可调参数M 和h,且具有明确的作用范围,因此,参数整定十分方便。
2 数值仿真
为了分析NTD 的性能及作用效果,在MATLAB的SIMULINK 环境下,建立了NTD 的仿真模型。仿真时采用0.002 固定步长、ODE1(Euler)算法,初始状态均为零。
为了验证速度因子M 的作用,取NTD 模型的输入为位置斜坡信号,其微分的结果相当于一个速度阶跃信号,图1 是h 为定值0.008,而M 分别取15、50、100 时的速度阶跃响应曲线,说明调节M 值可以控制跟踪微分器的响应速度,M 越大,跟踪速度越快。由于跟踪微分器使用了非线性环节,可以实现速度阶跃信号的快速无超调跟踪。
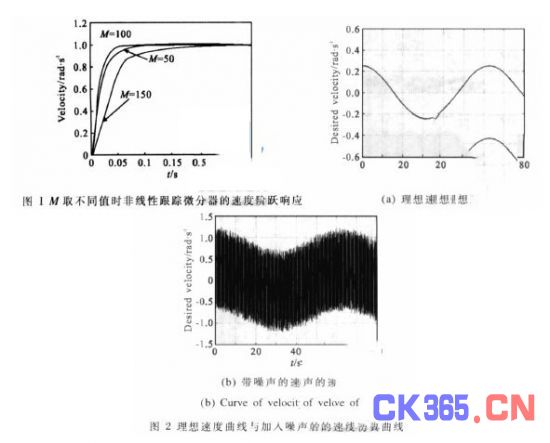
为了仿真NTD 的噪声抑制能力, 取输入位置信号为正弦曲线,其运动方程为θ =2.5sin(0.1t) rad, 对应的速度变化为ω=0.25cos(0.1t) rad/s,假设位置测量时引入幅度为0.001 rad 均匀白噪声,为了简化分析,仿真时忽略了量化误差的影响。图2 是真实的速度曲线与位置经差分获得的速度曲线,可以看出:后向差分算法对噪声有明显的放大作用,而这一现象在采样频率提高时尤为明显。
将上述加入噪声后的位置信号输入NTD, 经NTD 估计出速度及速度误差曲线,如图3 所示。由于参数决定NTD 的跟踪速度, 实验主要仿真了滤波因子h 的作用,图3(a)是取M=40、h=0.008 的仿真结果,图3(b)是取M=40、h=0.02 的仿真结果。可以看出:当h=0.008 时, 速度估计误差小于±0.05 rad/s; 当h=0.02时,速度估计误差小于±0.015 rad/s,可见,通过提高h值,可以明显改善噪声抑制能力。但h 并不是越大越好,h 越大,造成速度估计的相位损失也越大,通常取h=2T~10T,其中,T 为采样周期。对于M 和h 的选取原则,参考文献[11-13]给出了详细的说明。

3 实验验证
为了验证NTD 的实际应用效果,在某型地平式天文望远镜的方位轴上进行了实验。整个实验装置由机械平台、直流力矩电机、PWM 功率放大器和全数字伺服控制器等组成,其中机械平台和电机直接耦合,伺服控制器以基于PC104 总线的嵌入式计算机为控制核心,完成速度、位置的双闭环控制。系统具体参数为:电机轴上总惯量J=410.2 kg·m2,电机反电动势常数KB =52.7 V·s/rad,力矩常数Km =52.6 N·m/A,电枢回路总电阻R=4.0 Ω,电枢电感L=0.030 H,反馈装置采用24位绝对式光电轴角编码器,控制系统采样周期为2 ms。本实验将伺服系统设定在速度环工作模式, 并采用PI调节器,其中比例系数KP =100,积分系数KI =180。
3.1 速度估计实验
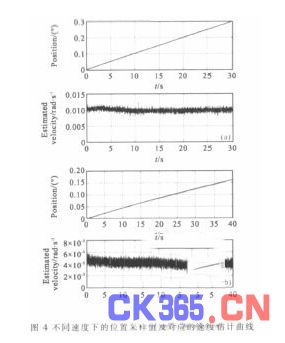
天文望远镜在跟踪星体时速度非常低,由于给定信号是数字量,当速度低到一定程度时,编码器输出的位置信号只能以一个码一个码的方式进行台阶式跳变,在跳变情况下,采用差分测速获得的瞬时速度会很大, 按照目前系统的配置, 速度的跳变量可达到0.010 7 (°)/s,严重影响低速测量的准确性。为了实时监控望远镜在跟踪状态下的角速度, 上位机常通过降低采样频率的方法来获得,而采用文中提出的方法,在不降低采样频率的情况下,仍能实时、准确地获得望远镜的运动速度。图4 就是望远镜速度分别设定在0.01 (°)/s(见图4(a))和0.004 (°)/s(见图4(b))时,编码器输出的位置信号以及通过此信号实时估计出的速度信号, 测试结果证明:应用所提出的方法可以实时、准确地估计出望远镜的转速信息。
3.2 低速跟踪实验
限于绝对式编码器的特性以及控制系统实时性的要求,伺服系统在提取速度反馈信息时,常采用的是一阶后向差分加低通滤波的方式, 低速跟踪时效果并不是很好。为了进一步验证文中方法的性能,将NTD 实时估计出的速度值直接作为反馈信号提供给伺服控制器,以检验它的实时性和准确性。实验时将望远镜的轴系运行速度设定在0.004 (°)/s,根据实际情况进行适当调整,取跟踪微分器的参数r=50,h=0.01。为了评价其作用效果, 上位机以10 Hz 的采样频率记录编码器的输出信号, 测量完毕, 再将测得位置数据进行后向差分,在不改变控制器参数的情况下,分别采用常规方法和文中方法得到的测试结果如图5 所示。
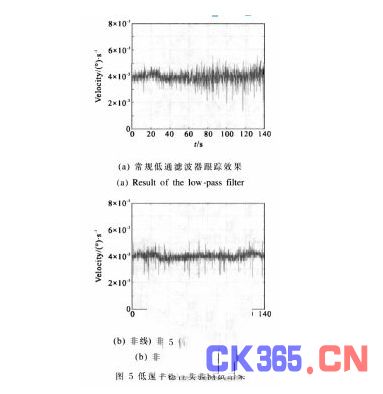
由测试曲线可以看出:采用常规方法时,速度波动较大,而采用文中提出的方法,尽管速度也存在波动,但波动的幅度明显小于前者,且速度更集中在0.004 (°)/s附近。经过对测试数据统计表明:采用常规方法的速度波动方差为1.563 (″)/s,而采用NTD 的速度波动方差降低到1.066 (″)/s,可见:NTD 的使用提高了速度测量的准确性,进而提高了伺服系统的低速平稳性。
4 结论
给出了一种基于位置测量的速度实时估计方法,既适用于增量式编码器,又适用于绝对式编码器。它采用对输入信号数值积分的方式,快速准确地估计出其微分信号,避免了常规差分算法带来的噪声放大问题;算法不依赖于对象模型,只有两个调整参数,且具有明确的作用范围,易于调节和实现。仿真分析表明:该方法能有效地降低编码器采样频率和测量噪声对测速的影响, 明显提高了低速测量的实时性和准确性,最后,在天文望远镜平台上进行了速度估计实验,并将此方法应用于系统的速度闭环反馈控制,在不改变控制器参数的情况下,将0.004 (°)/s 的速度波动方差从1.563 (″)/s 减少到1.066 (″)/s,改善了低速跟踪的速度平稳性。实践证明:该方法实时性好,易于实现,可以较好地解决光电编码器的低速测量问题。