1 引 言
火药药温是影响射程的实时变量,只能在发射现场实时确定。药温影响火药燃速,由此而对火箭飞行主动段终点诸元的影响,主要是通过比冲量和推力改变而体现的,引起vk、θk、yk、xk的变化,最终导致射程偏差[1]。对122 mm火箭弹[2,3],当最大射程为20 km时,药温相差10℃,射程中间误差EΔx=73~128 m;对40 km最大射程,药温每相差10℃,EΔx=180~204 m。对于最大射程为70~80 km的火箭,由射表计算得到,当药温相差10℃时,EΔx=400~700 m,仅此一项就远远超过了射程的1/220。显然,必须对药温进行精确的实时测量。
2 测量方法
箭药(推进剂)封装在发动机内,其温度随发动机壳体温度变化而变化。火箭弹在作战现场所处环境是随机的,依当时天候及贮存、运输条件而定。箭药表面要受环境对流和辐射换热作用,而自身温场应受热传导规律支配。因发动机壳体为合金钢,导热系数比火药大得多,且火药端部又存在隔热层。因此,箭药温度场比炮药的简单,可用柱坐标径向一维非稳态热传导方程描述。
对于这种比较典型的问题,用相似法测量其温度比较适宜,而不用炮药温度测量方法[4,5]以回避其测量装置结构复杂等缺点。采用相似法测量箭药实时温度,其关键是寻求一个与火箭发动机传热过程相似的多层壁面圆柱体,以保证描述它们传热过程的微分方程和单值性条件相同。由相似原理和无量纲分析可知,要满足相似条件,核心问题是必须保证傅里叶准则Fo和毕奥准则Bi均相等,即

式中:Fo=aτ/R2,Bi=αR/λ,下标m表示模型,下标p表示是原型,a为热扩散系数,a=λ/cρ,λ为物体导热系数,c为比热,ρ为密度,R为物体半径,τ为时间,α为放热系数。在所涉及的相关参量中,λ、c、ρ是物性,由选择的材料决定,R由几何条件决定,α由表面与环境的换热条件决定。
令ni为模型与原型的同名物理量i的无量纲比例系数。由式(1)及(2),比例系数群应满足:

于是,本测试问题转化为选择材料或人工制作材料,使式(6)和式(7)成立,最后用实验进行检验。理论上,箭药特征温度应取药温体积加权平均值。计算表明,相应特征点大约位于R/2~2R/3位置,具体与药型有关[8]。
3 基本构成及指标
本装置由测量用相似体(模型)和显示器两部分组成,后者带有数据显示窗,同时可加上RS232通信接口,将测量结果传输给火控计算机(详见图1)。其中相似体(模型)为60 mm×160 mm圆筒,显示器为110 mm×95 mm×65 mm的长方形盒体。本装置工作温度范围为-40℃~+60℃,在测量范围-40℃~+50℃及环境湿度为95%±3%条件下,系统误差不大于1℃。

4 实验验证结果及误差分析
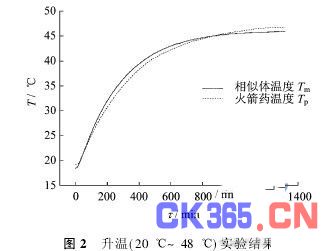

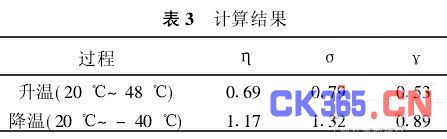
按相似法制作的1/5缩小尺寸模型与实物进行了两次验证试验,第一次是将实物和模型同时置入20℃的保温箱中,保持恒温12 h之后,再移入48℃高温环境,并保持20 h,采集火药在R/2~2R/3处的温度-时间(Tp-τ)曲线,与模型测试的温度-时间(Tm-τ)曲线比较见图2。另一次试验方法基本相同,只是保持环境温度为-40℃,Tp-τ曲线与Tm-τ曲线的比较见图3。图2和图3对应的数值(每隔30min采集1点)见表1和表2。分别计算算术平均误差η、标准误差(均方差)σ和概率误差γ:

计算结果见表3。

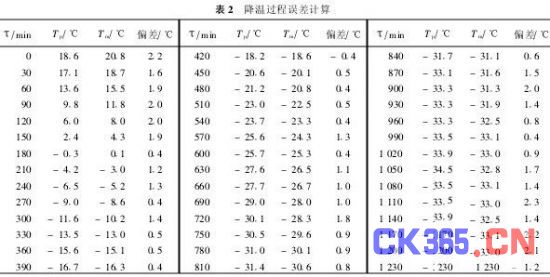
本装置的误差由显示器数据采集部分的误差和模型(相似体)部分的误差构成。其模型部分误差又包含相似模型引起的误差及测温探头误差。即数据采集误差ΔT1、相似体误差ΔT2及温度探头误差ΔT3,所以该装置的误差为
事实上,数据采集误差ΔT1很小,可略去不计。测温探头误差ΔT3理论上为±0·3℃,但低于-20℃之后这种探头不尽理想。因此,本装置的误差主要是由模型制作引起的,符合不大于1℃的要求。
5 结论
本文提出的火箭药温实时测量装置,体积小、精度高、价格便宜、结构简单、可靠性好。适用于各类无控或简控火箭武器系统弹道解算要求。