1 引 言
中国计量科学研究院在上世纪80年代,研制出一种沉浸式绝热式量热计,该量热计的工作范围为4·2~300 K,测量精密度高,但由于未得到经费支持,致使其没能投入使用。随着国民经济的发展,材料热物性测量标准的建立和量值溯源问题变得日益突出,而且国际计量组织也在近年来开始推进材料热物性测量国际比对工作。为了适应这些新的要求,作者对上述绝热式量热计进行了恢复使用和技术改造工作。工作的重点是将人工读取电参量数据改造为计算机自动精密读取,通过对测量结果与国外数据的比对和不确定度的分析,对改造后的量热计性能给出了定量的技术指标。
为了验证改造后量热计的性能,在80 ~275 K的温度范围内对美国国家标准技术研究院(NIST)的标准参考物质合成蓝宝石(α-Al2O3)进行了量热,从样品的热值得到材料的焓增,通过曲线拟合得到材料的焓增与温度的对应关系式,由此关系式对温度求导得到材料的比热值。与NIST公布的数据(ITS-68温标)[1]进行对比,焓增及比热值与NIST给出的数据的相对均方根偏差分别为8·62×10-3和4·47×10-3;样品材料的比热值与NIST公布的数据(ITS-90温标)[2]相比,其相对均方根误差为4·68×10-3;与文献[3,4]给出的比热值相比,相对均方根误差分别为4·80×10-3和4·77×10-3。本文给出的焓增和比热值多次测量数据的一致性用相对均方根误差表示,分别为1·46×10-3和1·67×10-3。
2 自动绝热量热计
2·1 量热计
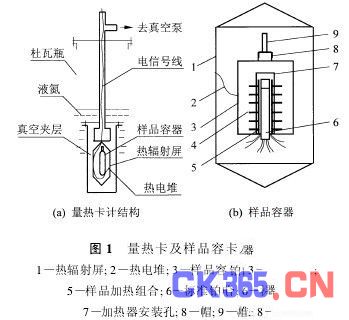
改进的自动绝热量热计完全继承了中国计量科学研究院在上世纪80年代研制的沉浸式绝热量热计的量热卡和本体结构[5]。量热卡计的结构见图1,样品容器为薄壁的圆柱形密闭容器,容积约60ml,外表面镀金以减少辐射换热。样品容器口用锡焊密封,密封后抽出内部空气,充入氦气,并将充入的氦气密封在样品容器内,以强化样品和样品加热器间的对流热交换。样品容器外有可跟踪样品温度的热辐射屏,样品容器和热辐射屏构成的系统置于一个真空夹层内,真空夹层被浸泡在液氮里。因此,热辐射屏是置于样品容器和液氮温度的环境之间。热辐射屏外表面均匀地布置有加热丝,与样品容器间有热电堆,热电堆的探测端和参考端分别连接在样品容器外壁和热辐射屏的内壁上,其电势差信号被送入控制器,控制器的反馈调节信号控制热辐射屏加热器电源,使得电势差信号始终趋于零。因此,通过这样的温度控制调节系统,热辐射屏的温度始终被控制,使其跟踪样品容器的壁面温度。
2·2 测量与控制
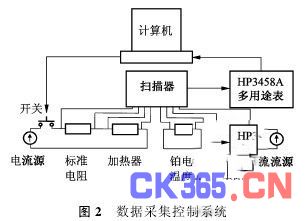
测量与控制系统的原理框图如图2所示。为了提高测量的准确性,用HP3458A多用途数字表作模数转换器,计算机控制低热电势自动扫描器。实验过程如下:扫描器根据计算机的指令自动扫描样品加热器、加热器回路标准电阻、铂电阻温度计、铂电阻温度计回路标准电阻,通过多用途数字表分别测量这些器件上的压降。在完成设定循环次数的加热过程后,计算机给出指令到继电器,令其关闭,计算机记录继电器关闭时刻。随后计算机给出指令,控制扫描器按相等的时间间隔读取铂电阻温度计及其回路上标准电阻上的压降,计算出铂电阻的阻值,计算两个相邻电阻值随时间的变化,在这个变化值小于设定值后,样品温度计所示温度为样品的热平衡温度。实验中样品被加热的时间为计算机记录的继电器开闭时刻的差,一般为20~40 min(温度越高,样品热容越大,加热时间越长),计算机能提供小于50ms的时间分辨率,因此,这种办法记录加热时间的相对误差不大于4·17×10-5。对样品的加热量是这段时间内加热功率的积分。从理论上讲,样品在两个相邻平衡温度间的焓增等于加热量。样品的温度用25Ω的标准铂电阻温度计测量,该铂电阻温度计根据ITS-90国际温标在中国计量科学研究院的低温三相点里分度,温度范围为13·803 3 ~ 273·16 K,扩展不确定度为1·6 ~0·22mK,覆盖因子为k=2·7~3·5。该铂电阻温度计和一等标准电阻及精密稳压电源串联,形成回路。回路中的电流小于1mA,标准电阻阻值的标准不确定度为1·5×10-6Ω。样品加热器也具有四线制结构,加热器、标准电阻和恒流源组成回路,计算机控制扫描器,分别读取加热器和标准电阻上的电压,通过这些测量值,可以计算出在某一段时间对样品的加热量。
用RS253控制器控制热辐射屏的温度,使其温度与样品温度一致。控制过程是:控制器读取热辐射屏和样品容器间热电堆的电势差,根据此电势差值,控制热辐射屏加热器电源的输出,从而达到控制热辐射屏温度的目的。此装置的热电堆由10个K型热电偶串联构成,热电堆在77 K和273 K附近的灵敏度分别为170μV/K和390μV/K。控制器RS253具有1μV的分辨率。因此,由热电堆和控制器组成的控制系统,从77 K到273 K具有5·6~2·6 mK的分辨率。实验中,热电堆测得的电势差被采集到计算机,以便评估热辐射的效应。
温度测量不准是量热计测量误差的一个重要来源。量热计温度测量必须考虑所测温度是否为被测样品的热平衡温度。为了得到热平衡温度,完成对样品加热后,需等待足够长的时间,否则,样品达不到热平衡。但若等待时间过长,又会因为漏热使所测温度偏离热平衡温度。对于本装置,被测样品达到热平衡的判别指标是对样品测温的标准铂电阻温度计的电阻随时间的变化率为5·0×10-6Ω/s。
3 量热实验
为了检验改进后的自动绝热量热计的性能,进行了一系列的量热实验。被测样品是NIST标准参考物质α-Al2O3(NIST的编号是SRM 720),样品的分子量是101·961 3。由于α-Al2O3在较宽温度范围内的理化特性极其稳定,因此广泛地用作标准物质。NIST和其它的实验室都公布了大量的这种标准物质的焓增和比热数据,将其用作传递标准,标定精度较低的科研和商业用量热仪器。NIST也用这种标准参考物质作为传递标准,比较不同量热计或同一量热计在不同时期的测量结果。测量实验按以下方法进行:对空容器和装有被测样品的实容器各进行三次量热测量,由量热结果得到被测样品的焓增值。样品的各次温升约为5K,被测样品的质量为66·482 g。实验测量的温度范围为80 ~275 K,对测量得到的焓增进行多项式曲线拟合,得到焓增与温度的曲线拟合关系式。为了得到更好的拟合,将拟合分两段进行,分别为80 ~170K和170~275K,拟合式对二阶导数光滑。拟合多项式的形式为

式中,Ai表示拟合多项式系数;ΔH为焓增,ΔH=H-H0,H表示测量得到的焓,H0是参考焓;T0为参考温度,对应于80~170K和170~275K,参考温度分别是79·021K和170·013 K;T表示样品的实际温度。
按定义,样品的定压比热是其焓值对温度的一阶导数,即
由式(2),通过焓增与温度的多项式拟合关系式对温度的一阶导数得到CP。
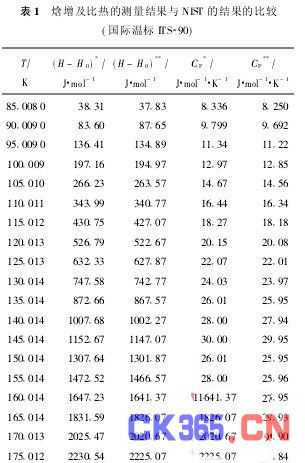
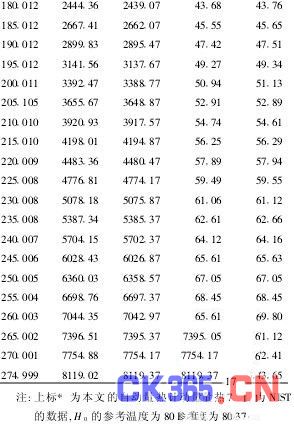
三次测量的热焓拟合值和导出的比热值与NIST公布的数据[1]列于表1中,温标是ITS-90国际温标。三次测量的焓增拟合值和比热值与NIST的数据[1]比较,相对均方根偏差分别为8·62×10-3和4·47×10-3。与NIST的比热数据[2]比较,相对的均方根偏差是4·68×10-3,温标基于ITS-90国际温标。本文的比热值及NIST的比热值[1,2]分别列于图3(a)和(b)中。在ITS-90国际温标下,比热值与文献[3,4]的结果相比较,相对均方根偏差分别为4·80×10-3和4·77×10-3。本文对不同实验测量结果的重复性进行了评估,三次测量的焓增拟合值和比热的相对均方根偏差分别为1·46×10-3和1·67×10-3。
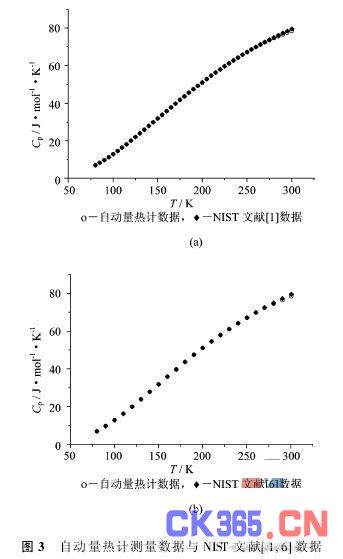
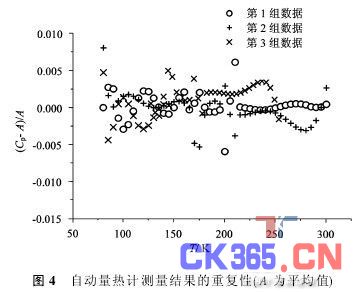
国外的量热实验[1~4,6~9]都是采取比对方法以证明测量结果的可靠性,最常用的比对样品是α-Al2O3。参考文献[1~4,6~9]中,比对的相对偏差大多在6·0×10-3的范围内,且文献[3,8,9]的比热数据都比NIST报告的数据[1,2,4,6,7]略偏高。从本文的实验测量结果与这些已发表的结果的对比可见,相对的均方根偏差与这些文献所报告的一致,说明改造后的自动绝热量热计装置与国外同类装置具有相同的测量精度。
4 不确定度分析
被测样品的焓增与作用于其上的热量的关系为
式中:Q1为对样品的加热量,Q2为辐射漏热,Q3为导热漏热,Q4为铂电阻温度计的自热。
样品容器及其热辐射屏间的热辐射可以通过记录热电堆的热电势差信号求得。热辐射的大小和控制器的性能以及样品所处温度有关。计算表明,样品温度接近于环境温度时,热辐射接近于零,而样品温度接近最高的加热温度时,热辐射最大,为0·004J/mol,与在这个温度测量的焓增相比,此辐射热太小可忽略。流过铂电阻温度计的电流低于1 mA,利用测得的流过温度计的电流值和电阻值,可估算出温度计的自热。在样品温度趋于300 K时,可以计算出铂电阻温度计的自热约为6·6×10-2J/mol,这个量与此温度的焓增相比,也可以忽略。如第二节所指出的,在完成对样品加热后的充分长时间的等待,是样品达到热平衡温度的关键。但是,因为样品容器的温度与其环境温度有比较大的差别,所以太长时间的等待会使样品温度因为导热漏热而明显偏离其热平衡温度。因此,导热漏热对量热测量的不确定度有贡献。通常绝热量热计的热焓测量分作两步,一是测量空容器,二是测量装有被测样品的实容器。实容器的测量值减去空容器的值就可得到被测样品的焓增值。
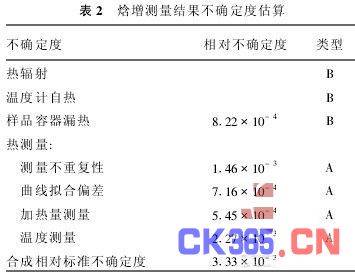
因此,被测样品的漏热是实容器的导热漏热减去空容器的导热漏热。实容器和空容器的漏热是分别测量的,因为辐射漏热在总的漏热中所占的份额很小,可忽略。因为是真空,对流换热没有作用,故认为所测的漏热就是导热漏热。漏热与样品温度和外界环境的温度差有关,漏热随样品温度与环境温度差的增大而增大,本文给出了样品温度在约170 K时的漏热对于相应温度焓增的相对值,分别测量实容器和空容器的漏热,得到实容器和空容器的典型值分别为2·88×10-4和1·11×10-3,实容器的漏热减去空容器的漏热可得样品的漏热,所得结果列于表2。热焓的测量误差是由多种原因造成的,如曲线拟合引起的偏差、测量结果的不重复性、样品温度测量误差、加热量测量误差等。表2给出了曲线拟合和测量结果的不重复性引起的不确定度。样品温度测量误差由恒流源输出的不稳定、多用途数字表的测量不确定度、自动扫描开关的寄生电势等因素引起。样品温度通过测量铂电阻温度计的阻值来确定,计算式如下:
式中:R为温度计的阻值、Vs0为标准电阻Rs0上的电压值。温度计电阻值测量不确定度及其带来的热流值测量不确定度可用式(4)求出,结果列于表2。加热量测量的不确定度也用类似的方法给出,加热量的表达式如下:
式中:Δt为加热时间间隔,Vh和Vhs分别为加热器和标准电阻Rhs上的电压。通过式(5),可以计算出加热量测量的不确定度。由于加热量测量的不确定度随温度变化,故表2给出了80 ~275 K的测量不确定度的最大值。
由式(3),焓增测量的合成相对标准不确定度为
式中:uc为合成相对标准不确定度,u1、u2、u3和u4分别为样品加热量测量、辐射热、导热漏热和温度计自热引起的不确定度,表2给出了合成相对标准不确定度的估算值,表明加热量和温度的测量对合成相对标准不确定度有重要的作用。因此,改善给样品加热器和铂电阻温度计供电的恒流源的性能,可以减少合成相对标准不确定度。
本文的焓增测量的合成相对标准不确定度的估算值为3·33×10-3。查阅国外文献,没有不确定度分析的资料,作者认为主要原因可能是因为测量结果的不确定度是随样品温度变化的,样品温度高,则均方根偏差小。本文所给出的是80 ~275K范围的合成相对标准不确定度,在样品温度较低时,测量结果的合成相对标准不确定度可能大于3·33×10-3,而样品温度较高时,测量结果的合成相对标准不确定度将小于3·33×10-3。合成相对标准不确定度3·33×10-3.根据定义,通过焓增对温度的导数求得比热值,很难直接估算出比热测量的不确定度,本文用相对的均方根偏差表示了比热测量值的重复性,其值为1·67×10-3。
5 结 论
本文报告了中国计量科学研究院用改进的自动绝热量热计进行实验的测量结果,测量NIST的标准物质SRM720的结果非常接近NIST及其它文献公布的数据。与NIST的焓增和比热数据对比,相对均方根偏差分别为8·62×10-3和4·47×10-3,本文的比热数据与文献[3,4]的比热数据比较,相对均方根偏差分别为4·80×10-3和4·77×10-3。改进的自动绝热量热计测量结果的重复性用平均值的相对均方根偏差表示,焓增和比热平均值的相对均方根偏差分别为1·46×10-3和1·67×10-3,在80 ~275 K的范围,其合成相对标准不确定度为3·33×10-3。从对测量结果的比较分析可以看出,自动绝热量热计的性能与发达国家的同类装置有可比性,可以用于精密量热。