0 引 言
NTC热敏电阻器除具有体积小、响应快、耐振动等优点外,还有阻值高、温度特性曲线的斜率大等特点。由于阻值高,往往可以忽略引线电阻的影响,即允许采用二线制接法。由于阻值随温度变化大,相应输出较大,对二次仪表的要求相对较低。缺点是量程窄、互换性差。
针对本文涉及研制项目温度测量量程窄、测量精度要求高(22℃±0.01℃)等特点,选用了经反复老化、长期稳定性指标优于0.002℃/a的热敏电阻器。尽管其阻值很高,仍然采用四线制的接法,以消除很小一点的引线电阻影响。对单支传感器进行了量程范围内多个温度点的严格标定。将其与采用特殊结构的
1 高精度温度测量系统的研究
1.1 数学模型
热敏电阻与温度的关系是严重非线性。为了对这种非线性进行尽可能准确的描述,采用了如下的Steinhart-Hart方程
式中 T为绝对温度值,K;R为热敏电阻器在温度为T时的电阻值,Ω。A,B, C,D则为4个特定的参数。一般需要采用多个温度点(至少4点)的标定获得热敏电阻器在已知温度点的阻值,然后,经过拟合获得模型的参数。这是一个从T和R出发推算A,B,C,D的过程,即校准或建模的过程。而测量时,则是在已知A,B, C,D的前提下,根据测出的R和数学模型推算出T的过程,这实际上是个内插的过程。
1.2 影响测量精度的因素
为了用热敏电阻器进行高精度的温度测量,必须研究各种影响因素,并采取相应的对策。在不考虑热敏电阻器的长期稳定性的前提下,尚有如下因素应当考虑:
(1)热敏电阻器的标定:从第1.1节的表述可以看出:高精度的测量实际是一个高精度的内插问题。而要进行高精度的内插,需要事先进行高精度的建模。而高精度的建模又需要依据高精度的标定数据、并经过可靠的数据处理后才能实现;
(2)激励电流的影响:电阻本身是不能直接测量的,必须对其供恒流电,然后,测其两端电压才能计算出电阻来。但这样做存在以下问题:因为精密的恒流源无法保证其真正“恒”流。从严格意义上讲,电流难免会因环境(如温度)的因素而发生一些微小的变化。即便这种变化可以忽略,但为了从电压计算出电阻,还必须知道激励电流的准确数值,这又涉及到对电流进行更高精度的测量,而这是极其困难的;
(3)热电动势:传感器在接入仪表的过程中不可避免会使用一些导线,经过一些节点。而这些导线几乎不可能是同一种金属构成的,且各节点也几乎不可能处在同一温度环境中。这样接点处就不可避免会产生热电势。而这些热电势将进入测温电路,影响到测量结果,使测量精度降低;
(4)自热效应、引线电阻、噪声和分辨力的影响:这些影响因素也是高精度温度测量中应该考虑的问题。
2 高精度温度测量系统的实现
2.1 校准和建模
选择0.01℃(水三相点)及25,30,32,37,60℃共6个温度点。除水三相点为额定温度值外,其余均用高精度恒温槽产生,其真实温度值(约定真值)用一等标准铂电阻作为上级标准读取。除此以外,为适应项目需要,将22℃作为测试检测点。
为了消除由温场波动带来的不确定性,传感器在上述6个温度点的每个温度点上分别进行600次测量取其平均值作为结果。在获得基本的标定数据以后,采用最小二乘法进行拟合处理,以获得Steinhart-Hart方程的系数。
所谓最小二乘法是指使实测数据和根据数学模型计算出来的理论数据之差的平方和为最小。这里的实测数据是指标定过程中测量得到的、与各已知温度点对应的电阻值,数学模型则是指Steinhart-Hart方程。根据最小二乘法,应有
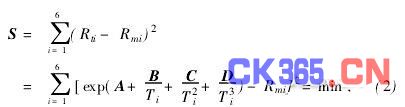
式中 下标t表示理论值;m表示实测值。由于上述方程的非线性,很难通过对其求导数推导出正则方程组。为此,对式(1)两侧取自然对数,并令x=1/T,可得y=1nR=A+Bx+Cx2+Dx3。这样,就重新给出最小二乘条件如下
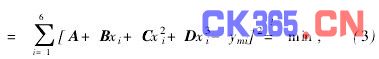
式中

式中 N为数据的点数,所有的连加运算均从1进行到N。这是一个线性方程组,由实测数据中的温度值和电阻值构成等号左侧的系数矩阵和等号右侧的列矢量。用矩阵求逆法不难求得参数列矢量,即A, B, C,D的具体数值来。这样,求出的结果是在式(3)定义的最小二乘意义下的最佳参数。但式(3)中的SL和式(2)中的S是有区别的,即,使SL最小的参数A,B, C,D不一定同时使S达到最小。其深层次原因是测量噪声的分布和影响因非线性变换x=1/T和
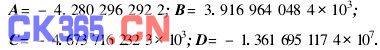
具体的实验数据、拟合数据和拟合误差见表1。
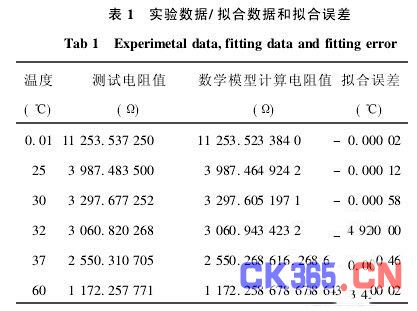
可以发现:在32℃点拟合误差稍大一些。其原因可能是上述非线性变换引起的。但不管怎么说,总体拟合精度还是相当好的。当然,为了保证数学模型长期可靠,应当定期(如,每年一次)对传感器进行校准,并重新进行参数拟合。通过Matlab软件得该热敏电阻器的电阻-温度拟合曲线如图1所示,
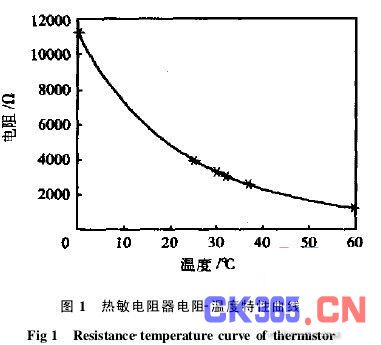
2.2 不利因素的消除
2.2.1激励电流影响的消除
为了消除激励电流的影响,测温仪并不直接依赖于对测温电阻两端电压的测量精度,而是在仪器内部装入了预先标定过的参考电阻。将外置电阻(测温电阻)和内置参考电阻串联供以同一电流,通过继电器切换分别测出各电阻两端的电压降。然后,比较这2个电压值得到比值,由于供电电流是一样的,这一比值就是外置电阻和内置参考电阻的比值。通过将内置参考电阻乘上这一比值就得到外置电阻的阻值,即
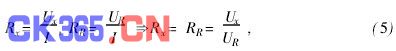
式中 下标x表示外置待测参数;下标R表示内置参考参数。基本测量电路如图2。
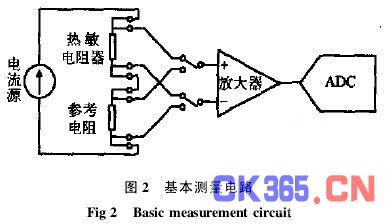
采取这样的措施后,不必知道恒流电流的具体数值,因为它并不出现在具体计算中。也不要求恒流电流具有长期稳定性,而只要求该电流在继电器切换阶段并未改变即可。
通过这一方法,还可在一定程度上避免由放大器和A/D转换器的波动或不准确造成的误差,因为这些误差是同时作用于外置电阻和内置参考电阻的。
2.2.2热电动势作用的消除
(1)使用交流激励电流,并使用只检测交流信号而抑制直流电动势的测量电路;
(2)定期关闭传感器电流,并直接测量热电动势。这种方法的问题在于,施加在传感器上的激励电流变化而导致的自热效应变化,从而导致误差;
(3)测温仪对外置电阻和内置电阻2个电阻均进行两次电压的测量。一次电流正向流过;一次电流反向流过。由于这2个电压测量值(短期内)是恒定的,因此,将它们相减就可以消除偏移电压(包括由热电势产生的偏移电压)。
具体来说,每次测量需要测量4个电压值,即,外置电阻(传感器)在正向供电时的电压
相比而言,第三种方法较为简单、可行。
3 结 论
在满足一定先决条件的前提下,采用热敏电阻器可以进行很高精度的温度测量。使用这种传感器最大的好处是输出大、耐振动,可以方便地用较长的引线安装到设备上。本应用研究中,使用的热敏电阻器经过与标准铂电阻温度计反复比对,在22℃时,连续几天内温度示值差不大于0.001℃,满足了控温系统的需要