0 引 言
热电偶作为测温传感器,其结构简单,测量准确度高,在自动测温系统中得到了广泛的应用。对于新研制的热电偶必须经过分度实验,在得到分度表及热电性能的温度曲线或参考函数后才能使用。由于受环境等影响,热电偶在使用一段时间后,其特性会发生变化,当热电特性变化超过规定的范围时,热电偶指示的温度便会失真,测温误差会越来越大。因此,对热电偶校准的研究就具有一定的意义。
1 RBF神经网络模型及学习规则
RBF网络由3层组成,结构图[1]如图1所示。输入层节点只是传递输入信号到隐含层,隐含层节点由像高斯函数的辐射状作用函数构成,而输出层节点通常是简单的线性函数。
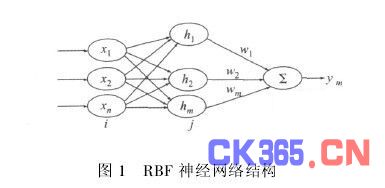
隐含层节点中的作用函数(核函数)对输入信号将在局部产生响应,也就是说,当输入信号靠近该函数的中央范围时,隐含层节点将产生较大的输出。由此可看出这种网络具有局部逼近能力,故径向基函数网络也称为局部感知场网络。
设有N个训练样本,则系统对所有N个训练样本的总误差函数[1]为:
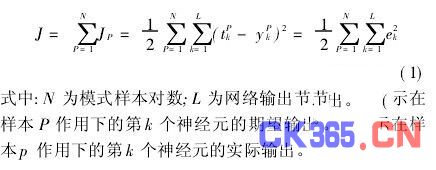
2 热电偶E-t特性神经网络模型
热电偶作为测温传感器,在工业测温系统中得到了广泛的应用。热电偶的特性,即输出的热电势E与温度t之间的关系是非线性的。对E-t关系,即热电偶分度表,传统的做法是采用查表法,但这种方法占用较大内存,因此一般采用数学建模的方法,通过建立热电偶E-t数学模型,实现热电势与温度的转换,以提高其测试精度。热电偶E-t特性的数学模型,通常采用的形式有分段线性拟合和分段多项式拟合两种形式,这两种形式都采用分段逼近的方法,建模方法简单,但计算量较大,适应性不好。而神经网络具有高速并行计算能力和非线性变换特性,能够随时进行学习,且学习效率高。相对于一般的建模方法而言,神经网络方法无须深入了解对象的机理,得到的数学模型表达方式非常简单。
用RBF神经网络建立热电偶神经网络模型。模型有3层组成,即输入层、隐层、输出层。热电偶输出的电压信号Vi为神经网络模型的输入,第i个隐层节点的输出为Ri,Wi为模型的权值,模型的输出为温度T。其中隐层节点的函数采用高斯函数。第Ri隐层节点的输出[1]为:

RBF网络的学习过程分为2个阶段[2]。第一阶段根据所有的输入样本决定隐含层各节点的高斯核函数的中心向量ci和标准化常数σi。第二阶段在决定好隐含层的参数后,根据样本,利用最小二乘原则,求出隐含层和输出层的权值Wi。在完成第二阶段的学习后,再根据样本信号,同时校正隐含层和输出层的参数,以进一步提高网络的精度。
工业过程中,通常对于热电偶的电势与温度的转化关系,采用的近似公式[3]为:

表。这里选用K型热电偶的分度表作为分析对象。RBF神经网络模型的建立中,取K型热电偶传感器冷端温度为0℃,热电偶热端温度变化范围0~1 370℃。在标准分度表中,从0℃开始,每5℃取一组数据,共选取260组数据,建立神经网络训练样本。然后对输入数据首先做归一化处理,进行网络训练,对输出的结果再反向复原,得到相对应的温度值。
在建立起RBF神经网络后,分别用RBF神经网络输出预测的结果和按照近似式(4)计算的结果,与国际电工委员会(IEC)给出的标准分度表相比较,其残差曲线如图2、3所示。
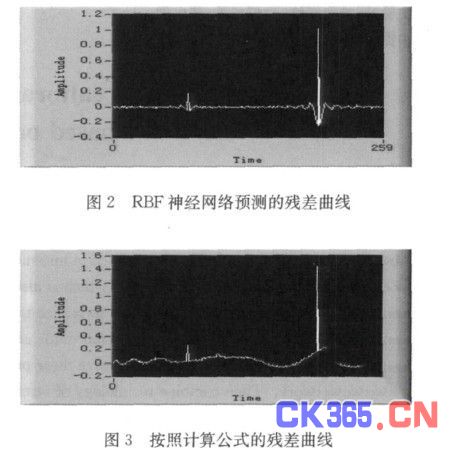
从图2和图3可以看到,RBF预测的结果与标准分度表的差在±0.02℃范围内,并且整体RBF的输出预测值比近似公式计算所得结果误差小。
3 用LabVIEW实现神经网络控制的热电势与温度的转换
实现热电偶的在线检测和校准,要有一个好的软件平台,这里选用LabVIEW[4]作为开发软件。在LabVIEW中实现神经网络,可通过多种方式[5]实现,如利用MAT-LAB Script节点编辑或调用MATLAB程序;利用Lab-VIEW本身的图形编程语言实现等。在热电势与温度的转换模型中,利用LabVIEW提供的MATLAB Script[6]节点,自动调用MATLAB,在MATLAB Script节点中编辑MATLAB程序,并在LabVIEW环境下运行。用LabVIEW7.1图形化编程语言[5]实现神经网络控制的热电势与温度的转换,其部分框图程序如下:
4 结束语
虚拟仪器与神经网络技术相结合,实现热偶热电势—温度分度的转换,与传统测试方法相比,此方法只需存储网络的权值和阈值,程序实现简单,速度快,精度高。并已在实际测试系统中得到应用,效果比较好。