1 前言
目前,铁路系统对车辆轴承表面缺陷进行无损检测普遍采用的方法是磁粉探伤法。作者与太原铁路分局车辆段合作,探索了一种利用误差分离理论对铁路轴承表面缺陷进行涡流无损检测的新方法和新技术,这对保障行车安全,提高生产效率,降低探伤成本,减轻劳动强度和改善工作条件有重要的价值。
关于误差分离技术和涡流无损检测技术的研究是在圆度测量和无损检测两个领域中分别独立地进行的。本文首次提出了把这两种技术结合起来对轴类工件表面进行无损探伤的四点法数学模型,并在此基础上建立了实验系统,对这一新方法进行了实验验证。实验结果表明这一新方法具有可行性。用涡流对轴类工件的表面缺陷进行无损检测,首先要解决工件的圆度误差和检测装置的主轴回转误差对表面缺陷信号的干扰,这就要涉及误差分离理论[1~5]。应用误差分离理论对轴类工件表面缺陷进行涡流无损检测的方法和技术,不仅是一种检测轴类工件表面缺陷的快速可靠、分辨率高的新方法,而且,还可以解决深孔内表面的无损探伤难题。涡流检测技术是一种正在兴起并逐渐发展的无损探伤技术。由于涡流对各种缺陷比较敏感,且具有体积小、结果可靠、不损坏试件和成本低廉等特点,因此有广阔的发展前景。目前,国内涡流检测的研究重点主要是在定性分析方面,主要是信号处理、分类和频谱分析等方面的信息积累工作;在定量分析方面也开展了一些工作[6,7]。
2 提取轴类工件表面缺陷信息的四点法数学模型
首先介绍误差分离三点法数学模型。如图1所示,设置于同一平面内理想的旋转中心O点,以之为原点,作与三测头固联的静直角坐标系XOY,使X轴与传感器A的轴线OA重合,设∠AOB=α,∠BOC=β,视被测工件做刚体平面运动,取工件主轴系统的瞬时旋转轴中心O′为极心,做极坐标系与被测工件固联,极角θ逆时针取向,以S(θ)标识工件的轮廓曲线(工件的圆度误差),以RX(θ)和RY(θ)标识极心的平动,即主轴回转误差在水平和垂直方向上的分量,工件的运动就可以用工件瞬时回转中心在静直角坐标系中的平动和工件本身在极坐标系中的转动来描绘它。
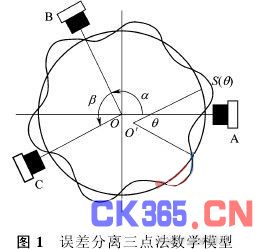
这样就可以得到三点法误差分离的原始方程



这样,利用误差分离技术,在一次安装中拾取不同方位的三个传感器的采样信号,即可同时求得工件的圆度误差和该时间样本上的主轴回转误差。
在基于误差分离理论提取轴类工件表面缺陷信息的四点提取法数学模型中,三个用于获取误差分离计算所需信号的传感器测头A、B、C在安装方法上,同三点法误差分离理论的数学模型不同(如图2所示),传感器A、B、C与被测工件之间各通过一金属块的传递同被测工件相接触。这样,传感器A、B、C的输出信号中就可以只包含工件的圆度误差和检测装置的主轴回转误差,而排除了包括表面缺陷信号在内的其它综合信号的干扰。此外,需再安装一个与被测工件非接触的传感器,其输出信号中不仅包含了被测工件的圆度误差和检测装置的主轴回转误差,而且还包含了包括工件表面粗糙度在内的裂纹、淬火(硬度、结晶结构)不均匀等各种表面缺陷的信息,故称为综合信号传感器S。从其采样信号中分离掉工件的圆度误差和检测装置的主轴回转误差后,便可以获得反映表面缺陷的信号。
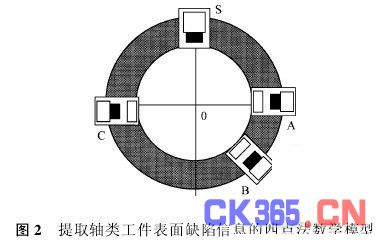
在这个数学模型中,传感器A、B、C的安装角度以及静、极坐标系的构造方法与在误差分离理论的数学模型中完全相同,传感器S的安装角度应在2π/64的整数倍相位上。这样就可以得到四个传感器输出信号的原始方程:
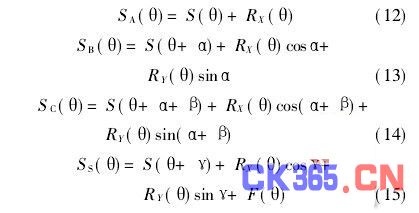
其中,SS(θ)为综合信号传感器的输出(已去除直流分量,即平均分量),F(θ)为缺陷信号,γ为传感器A和S沿逆时针的夹角,其余同误差分离三点法。这样,应用三点法误差分离理论就可以解得被测工件的表面缺陷结果如下:
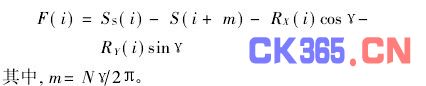
3 实验系统与实验结果分析
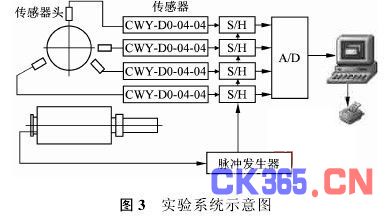
3·1 实验系统的工作原理
实验装置包括数据采集子系统和数据处理子系统两个部分。如图3所示。数据采集子系统由传感器支架、传感器供电电源、测量装置、工件旋转装置、分度装置和A/D转换装置构成,在微机的控制下,完成对被测工件的圆度误差、检测装置的主轴回转误差和被测工件表面缺陷等原始信号的数据采集工作。数据处理子系统由一台微型计算机和打印机组成。完成对原始数据的采样控制、误差分离、表面缺陷的提取、频谱分析和作图打印等工作。
3·2 实验步骤
(1)对被测工件重复测量,获取单截面的20圈采样数据,经误差分离后对分离结果作统计分析,以检验实验系统的复现性。
(2)以每次5 mm的步进长度,沿轴向对被测工件进行10个截面的测量与误差分离,分析其波形图、频谱图和模拟图,以验证分离结果是否符合理论分析的结论。
(3)取有和无表面缺陷的轴承滚子各一个,以每次5 mm的步进长度各作10个截面的测量与误差分离,对比分析,以验证轴类工件表面缺陷信号四点提取法数学模型的可行性。
(4)对被测工件的圆度误差、检测装置的主轴回转误差和被测工件表面缺陷的分离与提取结果作波形分析和频谱分析。
3·3 实验结果与分析
(1)对被测工件某截面重复进行20圈数据采样,经误差分离后对分离结果作统计分析。结果表明,测量以系统误差为主,随机误差很小。这表明实验系统具有良好的稳定性和复现性。图4和图5分别是被测工件形状误差和检测装置主轴回转误差的模拟图及频谱图。


(2)对同一轴承滚子的同一截面,实验系统和圆度仪测得的圆度误差相对偏差未超过2%。这表明误差分离理论的基本原理是正确的。
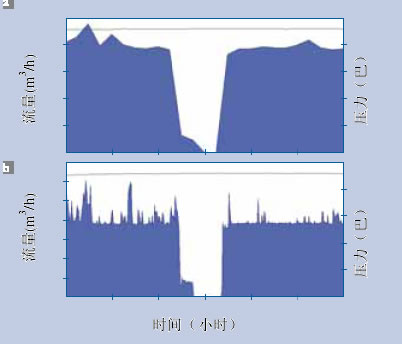
(3)有表面缺陷和无表面缺陷轴承滚子测量结果的对比见图6。无表面缺陷轴承滚子的模拟图与基圆基本重合,而有表面缺陷轴承滚子的模拟图则表现出了较大的波动性,有缺陷轴承滚子的频谱明显丰富。显然,被测工件的表面缺陷信息被提取出来。可见,轴类工件表面缺陷四点提取法的数学模型是充分可行的。在有表面缺陷的频谱图中,高频成份约占全部谐波成份的20%左右,似可归因于表面粗糙度的影响,而认为表面粗糙度也在其中得到了一定程度的反映。其余振幅较大、振动频率较低的部分可以认为完全是表面缺陷的反映,其谐波成份占全部谐波成份的80%,其中以2~10次谐波为主,占到全部谐波成份的60%。
4 结论
从实验结果可以得到以下结论:
(1)通过对有表面缺陷和无表面缺陷轴承滚子测量结果的对比分析,证明了应用误差分离理论提取轴类工件表面缺陷信息的方法是可行的,也为今后研究奠定了基础。
(2)本实验系统用微机进行实时数据处理,可以实时在线地快速分离出被测工件的圆度误差和实验装置的主轴回转误差,并能在此基础上提取出表面缺陷的信息。与圆度仪相比,其检测效率可提高95%,成本降低90%以上。其必要的数据输出和直观的图形表示,可用于对加工圆度的评定、对加工误差的分析和对轴类工件表面缺陷的检测。为圆度误差的测量,为进行轴类工件表面缺陷的定性分析和分类研究提供了一种测量精度高、操作方法简单、成本低廉、性能稳定可靠的新型测量分析系统,也为超精圆度的测量和评定工作提供了新的有效的研究手段。
(3)对测量结果分析所得到的有关加工圆度误差、回转误差和表面缺陷信息的数据特征、波形特征、频谱特征和模拟特征,有一定的参考价值。