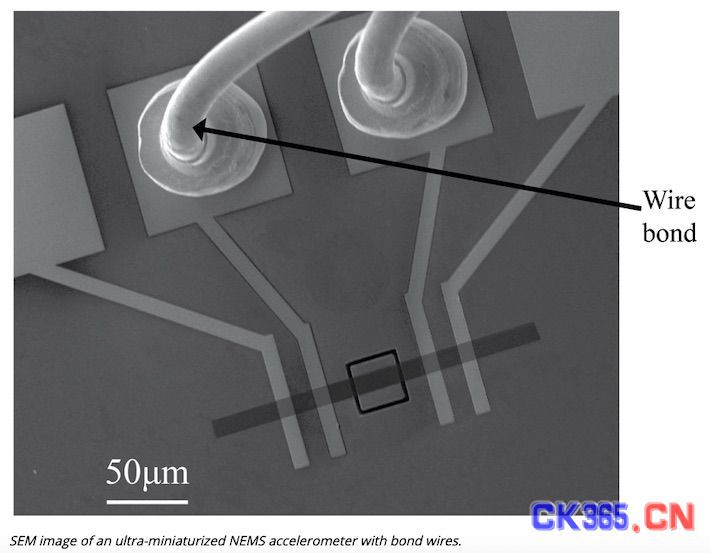
残余应力 发生在任何机械结构中. 产生的原因,如焊接和塑性形变或材料的局部变形,材料表面的尖锐凹槽或者是敲击,或硬化等.
残余应力和机械应力对于机械结构来讲都一样重要. 但是,与机械应力可以通过加载来进行计算不同,因此,残余应力需要采用可靠的方法进行测量,而不能对表面产生大的破坏.
这也是钻孔理论产生的原因。通过在应变花的中心在材料表面钻个非常小的孔,通过检测在钻孔前后,应变花的变化,可以计算出残余应力的大小.
MTS 3000 系统包括:
一个光学-机械系统 (进行物理钻孔) 一个电子控制单元(控制光学-机械系统并通过HBM Spider8-30 放大器进行测量) 钻孔操作和控制软件 (进行自动钻孔) 后处理软件 (采用不同的评估理论来处理数据).
采用气涡轮进行钻孔,转速可达 400,000 RPM ,因此不会产生额外的残余应力.
后处理软件用来计算残余应力.
获得精确的应力状况,计算方法是非常重要的 许多研究者发表了很多钻孔理论计算应力的文献.
目前,在后处理软件中有三种计算方法: 均一应力理论, Kockelmann 理论和积分法 .
均一应力理论 [ASTM E 837-01标准]
这种理论在 ASTM E 837-01 标准中进行了详细描述, 是基于样本表面应力不伴随距离变化的假设为基础的. 因此,不考虑空间解析度. 如果残余应力是均一的,这是最好的计算方法,并且对测试错误不敏感.
Kockelmann 理论
Kockelmann 理论是建立在应变导数和应变分布存在相关性的理论基础上的,通过洞深度函数来表达. 通过一对系数(Kx and Ky), 通过仿真模型来进行计算.
通过应变值,以及摩尔圆来计算主应力和方向是可能的.
积分理论
此方法是有 G. S. Schajer 提出, 通过钻孔深度增加来进行残余应力分析. 采用这种方法,通过同步所有深度应力释放比其他方法有更高的空间分度.
为了简化残余应力计算, Schajer 提出应力区可以通过 step-wise 函数描述,其通过孔深度是恒定的. 采用这种假说, Schajer 建立了计算的协同系数. 最大深度为应变花半径的 0.5 倍.
积分理论应当在随洞深度不同,应力有很大变化时使用,但其测试误差也有很到灵敏性.
最新! ASTM E837-08
这是计算非均一残余应力的新标准. 积分法用于残余应力计算, Tikhonov 规则用于在使用大量的不同洞深度时来减少计算误差.